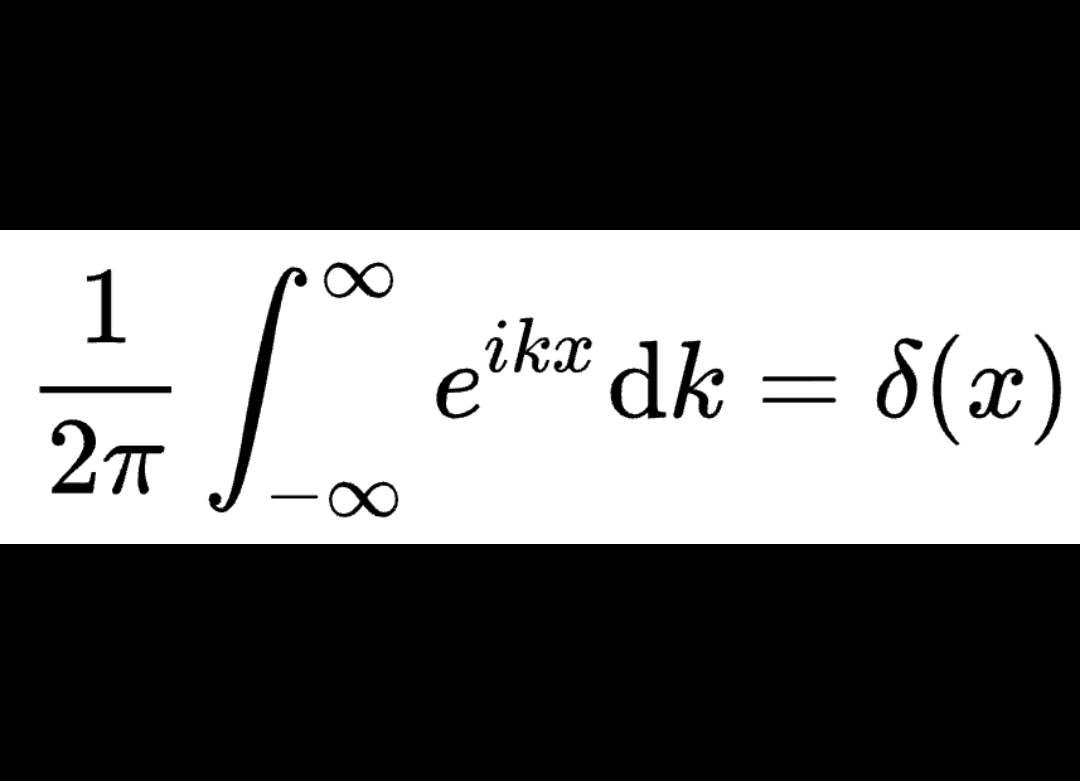adad8mπ¦
@adad8m
Followers
9K
Following
14K
Media
1K
Statuses
5K
When you discover that any element in a finite group has a finite order π
.
25
554
5K
"[Henri PoincarΓ©] worked regularly from 10 till 12 in the morning and from 5 till 7 in the late afternoon. He found that working longer seldom achieved anything"
46
433
3K
A few years ago, #Singapore Prime minister Lee Hsien Loong wrote and shared a C++ Sudoku solver, how cool is that! π
. Not much comment in the code, but it's available here:
44
327
2K
Fit a polynomial of degree D to N points by minimising the mean squared error. Now, start increasing D and look at the accuracy. The accuracy blows-up around D~N and starts improving *again* for D>>N π. #doubleDescent #statistics #maths
32
248
2K
What happens when you do PCA on a few Brownian trajectories. As the number of trajectories increases, the Principal Components converge to sine waves. #statistics
Interesting! I hope it's not just SVD/PCA on almost random noise because it's likely to have found similar patterns. (ie. you get sine waves when doing PCA on noise) #Statistics.
47
264
2K
Oh, that's why! π
Shampoo Scaling law for language model.Plot taste of Kaplan et al, but comparing shampoo and adam. Shampoo is literally such a free lunch, in large scale, in predictable manner.
2
106
2K
18
93
2K
This Barzilai-Borwein stuff is crazy, it's just choosing a slightly clever stepsize (i.e. no preconditionning) and is doing so much better than gradient descent with backtracking line-search! Still blowing my mind, who has some good readings about that? .#optimization #maths
BarzilaiβBorwein method selects the step size for a gradient descent using a cheap approximation of the Hessian. Performs usually better than line search.
13
101
1K
One of the best books to learn probability, I did spend many hours on that one! What are some similar exercise books that cover a large part of (insert another topic)? #books.
3) One Thousand Exercises in Probability by Geoffrey Grimmett and David Stirzaker. This is evergreen. Learning how to do Markov chains and solve the eigenvalues will never, ever not be helpful. This stuff requires more energy to read, but it keeps you sharp.
12
78
977
That's the characteristic polynomial of a random matrix . M β R^{300 x 300}. Guess how the matrix was generated?.#maths #probability
21
85
907
Even AI doesn't believesitπ
BREAKING NEWS.The Royal Swedish Academy of Sciences has decided to award the 2024 #NobelPrize in Physics to John J. Hopfield and Geoffrey E. Hinton βfor foundational discoveries and inventions that enable machine learning with artificial neural networks.β
12
131
916
Graphical comparison between the standard (linear) #correlation and the Chatterjee's "rank correlation" recently introduced in #statistics #probability @johnleibniz @_bakshay
14
220
886
Glad to announce I'm joining in September 2023. Our goal is to understand the universe, regulate the use of gzip and prevent human extinction. #AI.
this is wild β kNN using a gzip-based distance metric outperforms BERT and other neural methods for OOD sentence classification. intuition: 2 texts similar if cat-ing one to the other barely increases gzip size. no training, no tuning, no params β this is the entire algorithm:
13
55
797
Read yesterday in a ML paper (forgot which one). "One can approximate a Dirac delta function with a Gaussian distribution with variance zero".
29
63
770
Over the past few weeks, I've been reading some parts of this Linear Algebra #book & the author emphasises block matrices computations, which is quite different from many other textbooks and also surprisingly powerful. Recommended!.#maths
A few favorite related refs:. 1. Axler's preface in "Linear Algebra Done Right", suggesting par at 1 page/hour. 2. Norvig's "Teach Yourself Programming in Ten Years" (contra Learn C++ in 24 Hours)
6
83
739
Arrived today β€οΈ will try to share short #simulations as I go through it π. #book #statphy #maths
10
92
721
4
83
625
@dieworkwear If you need a full Twitter thread to explain why something looks great, does it really look that great?.
265
10
559
Reading list of January π.Week 1. "Gravitation", Misner & al.Week 2. "Modern Classical Physics", Thorne.Week 3. "Introduction to Differential Geometry", Spivak.Week 4. "The Road to Reality", Penrose. Will start Landau & Lifshitz if I still have a bit of time.
45
38
563
Finally had time to try one of these #KAN architectures. Surprised how well it worked on this low-dim regression example. For a #MLP to converge that fast, it would typically need a bit of feature engineering (eg. Fourier features, etc. ) Good stuff!
MLPs are so foundational, but are there alternatives? MLPs place activation functions on neurons, but can we instead place (learnable) activation functions on weights? Yes, we KAN! We propose Kolmogorov-Arnold Networks (KAN), which are more accurate and interpretable than MLPs.π§΅
9
51
519
The Cayley transform. C(z) = (z+i)/(z-i). maps the upper complex plane onto the unit disk. #complexAnalysis #maths
The Mobius transform . F(z) = (z-z0) / (z*conj(z0) - 1). maps the complex unit disk into itself. It is an involution that exchanges z=0 and z=z_0, and it's beautiful π. Except the usual Schwarz lemma, what are some cool applications of these transformations?. #complexAnalysis
4
76
499
I'm visiting my parents today and I just bumped into two very old friends.
8
21
503
I am a fan of the (β€οΈHessian freeβ€οΈ) LevenbergβMarquardt method! Here it is on the Rosenbrock function π. #optimization #math
Barzilai-Borwein method selects the step size for gradient descent using a cheap approximation of the Hessian. Performs usually (much) better than line search.
4
74
483
We understand Newton's method π.
Whoever tells you βwe understand deep learningβ just show them this. Fractals of the loss landscape as a function of hyperparameters even for small two layers nets. Incredible.
10
25
469
greedy search is enough.
My daughter had a nice problem in her high-school math club. Suppose you have 1000 white points and 1000 black points in the plane, no three collinear. Can you draw segments connecting them in pairs, from white to black, using each point just once, without any edges crossing?.
11
24
473
In high-dimensional spaces, a step in a random direction is more likely to take you further from the origin! There is a lot of space to explore in high-dimensions π
Probability of returning to the origin in a random walk:.1D β P=1.2D β P=1.3D β P=0.34.Large D β P=1/2D
14
51
467
@PreetumNakkiran proposed to look at the jpeg size per pixel to find the correct dimensions: works very well! . #statistics #maths
imagine we have a stream of pixels coming in one by one. They form a video, but we don't know the width and height of each frame. Here we try a bunch of guesses for the dimensions, before locking in on the correct values
7
51
423
This Kozachenko-Leonenko estimator of the #entropy is really neat! Animation below minimises the usual (Energy-Entropy) functional for a mixture of Gaussians π. Thanks to @gabrielpeyre and @sp_monte_carlo for making me discover this today #maths
@adad8m @gabrielpeyre i believe that the entropy estimator itself is called the Kozachenko-Leonenko estimator, see e.g. and the original paper (in Russian)
6
65
420
Interesting comparison of the KAN neural architecture when compared to standard MLP!
Itβs possible to rewrite a certain kind of complicated mathematical function as a combination of simpler ones. This discovery, made in 1957 by Andrey Kolmogorov (left) and Vladimir Arnold (right), is at the heart of a new network architecture that could make AI easier to study
6
57
430
Well, tbh, there is no very good reason to divide by (n-1). And I've never seen a practically relevant situation where this makes a difference. .
WHY do we divide by n-1 when computing the sample variance?. I've never seen this way of explaining this concept anywhere else. Read on if you want a completely new way of looking at this.
35
28
378
Interesting! I hope it's not just SVD/PCA on almost random noise because it's likely to have found similar patterns. (ie. you get sine waves when doing PCA on noise) #Statistics.
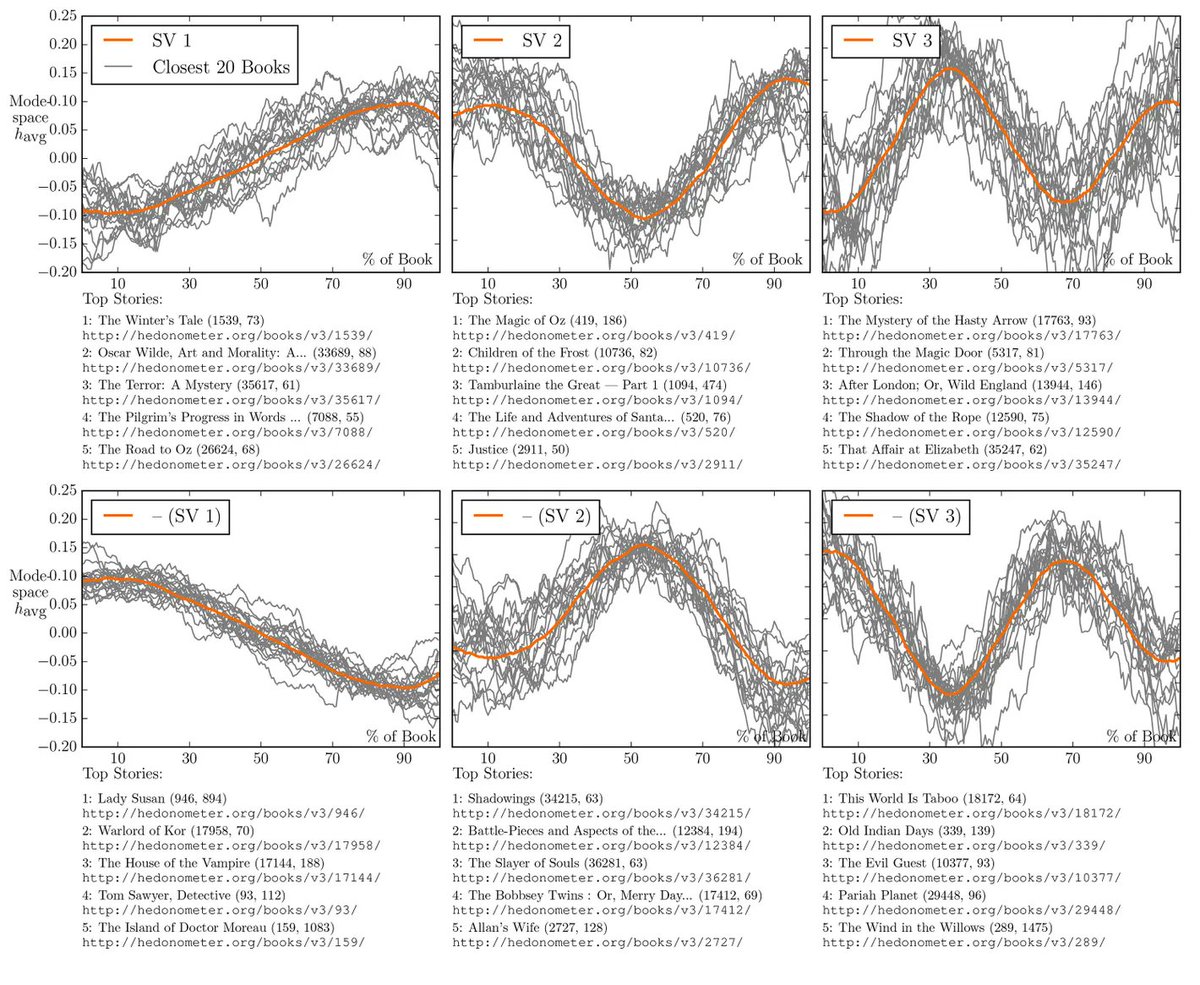
In 2016, researchers at the University of Adelaide tested Kurt Vonnegut's theory that, "Thereβs no reason why the simple shapes of stories canβt be fed into computers.". They took the emotional arcs of 1300+ novels fromΒ Project Gutenberg, turned that into data, used modern tech
12
18
379
Oh come on, is it the standard we expect from our Turing award winners nowadays? "True Bayesian", random nonsensical proba estimate that will change next week, etc.
32
13
334
Consider a 2-layered #neuralnet of the type. F(x) = (1/N) β a_i * ΙΈ(x-c_i). for some nonlinearity ΙΈ. During training, the empirical distribution of weights (a_i, c_i) can be described by a cute PDE and it's also quite interesting to visualize π. #maths #deeplearning
6
43
347
Twitter is such an amazing place! How fortunate we are to witness such profound scholastic debate by the intellectual giants of our times.
27
15
339
Seems like a very fun #complexAnalysis book, anyone has read it? I like it that it seems computational, with interesting simulations/computations to perform!.#maths #book
2
39
339
Challenge accepted! This looks like hieroglyphs to me, and hopefully not anymore in a few months time π
16
8
315
I'm a bit biased, but I'm still finding it funny to meet people who can talk to me about the Langlands programme and the Trace class formula but cannot do a linear regression or simulate a pendulum. I've met plenty!.
17
16
298
Fill 5x5 matrices with +1/-1 at random and plot the eigenvalues. Repeat many times. What's that structure?. #randomMatrices #maths
all the complex roots of degree ten polynomials whos coefficients are either 1 or -1
10
32
281
Interesting read: how to go from the slow matrix-multiplication #python code below that runs in 6h to an optimized code than runs in 1sec!
Matrix Multiplication: Optimizing the code from 6 hours to ~ 1 sec. "Performance Engineering is a lost art." - Charles Leiserson . I followed this lecture -
6
29
276
Take a 2D circle and propagate it through a fully connected #neuralnet whose layers have 256 neurons and randomly generated weights with std = Ο/β256. At each layer, visualise a (linear) 2D projection. What's the influence of Ο?. #maths #deeplearning
7
25
258
Recommended account to follow, with many wonderful youtube #maths videos!.
Why do we require Jacobi identity to be satisfied for a Lie bracket? In the process, we also understand intuitively why tr(AB) = tr(BA) without matrix components. Watch now:
8
17
236
The Mobius transform . F(z) = (z-z0) / (z*conj(z0) - 1). maps the complex unit disk into itself. It is an involution that exchanges z=0 and z=z_0, and it's beautiful π. Except the usual Schwarz lemma, what are some cool applications of these transformations?. #complexAnalysis
4
28
231
For two PSD matrices, is there a name for this quantity? That's the matrix that describe the optimal transport from two Gaussians.
14
17
232
Anti-social dynamics π
. Consider 100 persons walking at constant speed and always perpendicular to their closest neighbours. If there were only 2 persons, they would follow the same circle forever. More complicated with 100 persons π . Does it stay bounded? @johncarlosbaez
30
26
234
Variational inference: a Gaussian hesitating between two modes. π
. Details: SGD to minimize KL(q || target) with standard reparametrization trick. #optimization #maths #ML
2
15
233
Am in a hotel and there are a few old books on display in the reception hall. Always fun to see some old polymer chemistry
3
7
232
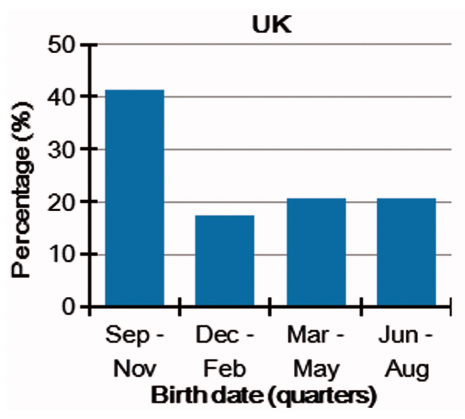
OK, this actually seems to be true that UK Nobel prize winners are more likely to be born in September: the question then is why? #Statistics .
3. Small advantages compound. This is why UK Nobel Prize winners are 2x as likely to be born in September. It's not the genes - just the small headstart of being developmentally a bit ahead is very potent academically.
88
25
225
Couldn't resist to reproduce @j_bertolotti fantastic experiment. Below, the eigenmode of N=100 coupled oscillators placed on a circle. Each oscillator is coupled to its 2 neighbours. As the masses get more random, one observe "Anderson #localization" π. #physics
2
20
198
For two matrices A and B of compatible dimensions and function f(. ) "nice enough" to be Taylor expanded we have the following identity, as a one line proof shows by expanding f(. ). Silly, but first time I am noticing it. Is there a name for this? Applications?
6
14
213
Physics 101 discussion:.Did this guy invent free energy? Who does the work when carrying the backpack up and down the mountain?.
47
11
205
Damn, MIT is overrated π
6
9
186
