This resonated with me in my Masters and it still does sometimes now

I'll probably watch Avatar twice in the cinema, because I really like popcorn

Ah! You see, this miserable little document, this so-called date-me doc, is our era’s most honest pornography. It pretends to be romance, but what is it really? It is no longer the trembling hand on paper, the confession of desire. It is a spreadsheet of desire. “I am ready. I am

Very cool Math/Phisics postdoc positions at OIST (Okinawa, Japan), to work with Matteo Parisi (who has worked extensively on Amplituhedra), who is starting a position as an Assistant professor there. Share this around to people that might be interested https://t.co/dVaGFvz7QB

https://t.co/Jid1xqo4Vb

So it's postdoc application season and I'll be applying! Woo! Pic unrelated

A really good introduction of generative models for a physics audience! It's also a big plus it's on a blackboard too. It feels more like a conversation than a talk

And this kind of proof also points at interesting papers. I arrived at Maskit's paper trying to understand when an M-curve admits another real structure that makes it an M-curve. It was only after reading Maskit's work that I realized I needed a result just like it! 2/2

Among proofs, this one is along the lines of "oh, I know this cool theorem in this paper... so what you want is an elementary corollary of this theorem." But I like elementary proofs, they can rapidly convince you of correctness :) 1/2

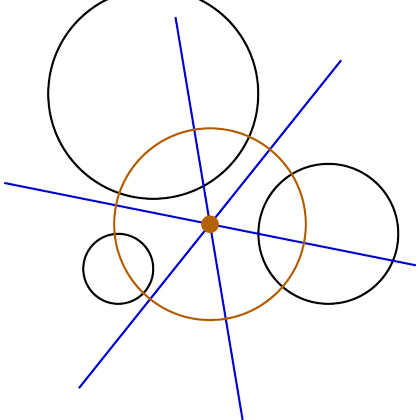
are nicely symmetric, and it's trivial to find *the* mutually orthogonal circle to g of the circles, which doesn't touch the lasts circle. But this only works if g>=3. But that's okay, every genus-2 Riemann surface is hyperelliptic :) 4/4

here: The Riemann surface is hyperelliptic if and only if there is a mutually orthogonal circle to all (g+1) circles. Classical geometry (see https://t.co/6HSZWLaarV ) tells us that 3 circles define such a mutually orthogonal circle. It turns out that our circle arrangements 3/4

The genus-g Riemann surfaces in question are described by disjoint circles on the complex plane (i.e. the data of a Schottky gorup). One needs g+1 disjoint circles and then finds the group by reflections across circles. Anyways! Maskit tells us that there is a nice check 2/3

A friend and I were talking about the favorite theorems we've proven in a paper. Mine concerns that a family of Riemann surfaces are non-hyperelliptic, and thanks to a result of Bernard Maskit [in "Remarks on m-Symmetric Riemann Surfaces"], it follows from nice geometry 1/3

Anything written in English in Japan is written in English for a reason

I just saw this position and have no connections to it, but I've been a Master's student in Sao Paulo, at the host of this position (IFT-UNESP, where ICTP-SAIFR is located), and can vouch for it being a great place to live and work :)

There's a cool joint PhD position between ICTP-SAIFR (Sao Paulo, Brasil) and SUNY (Buffalo, USA) on Quantum information (and thermalization, ergodiciy, non-equilibrium, thermodynamics, etc...). Do share it with people you know! https://t.co/ZE8tyXDZa9

Inspired by this thread, here is a thread on the complex analytic bump functions:

娘のデートに送ったら チェーンソーマン🇺🇸は17歳以下は親と観ないといけないらしく急遽私も観ることに💦💦 気まずい😅

i want someone to crawl inside of my mind and sift through every single memory i've ever had. i want them to know every thought that's crossed my mind. maybe then someone could finally understand what it means to be me other than me.

i LOVE saying "Same hat" it's from this comic strip Original by: Yoshida Sensha

ao3 (arXiv of our own)