Oswin So @ NeurIPS (Dec 2 - Dec 7)
@oswinso
Followers
172
Following
119
Media
9
Statuses
48
Graduate Researcher with Chuchu Fan at MIT @mit_REALM. Bringing Guarantees to Safe Reinforcement Learning 🇭🇰
Cambridge, Massachusetts
Joined April 2013
At #NeurIPS from Dec 2 to Dec 7 in San Diego! Looking forward to catching up and meeting new friends. Excited to chat about safety for robotics, constraint satisfaction in RL, and (stochastic) optimal control. Feel free to DM me to grab coffee or have a chat!
0
0
5
Robots can plan, but rarely improvise. How do we move beyond pick-and-place to multi-object, improvisational manipulation without giving up completeness guarantees? We introduce Shortcut Learning for Abstract Planning (SLAP), a new method that uses reinforcement learning (RL) to
1
20
65
Meet Casper👻, a friendly robot sidekick who shadows your day, decodes your intents on the fly, and lends a hand while you stay in control! Instead of passively receiving commands, what if a robot actively sense what you need in the background, and step in when confident? (1/n)
6
39
164
#almostsure blog post: On the integral ∫I(W ≥ 0) dW This looks at the mentioned integral, which displays properties particular to stochastic integration and which may seem counter-intuitive. https://t.co/gRRyvtNg2O
almostsuremath.com
In this post I look at the integral Xt = ∫0t 1{W≥0} dW for standard Brownian motion W. This is a particularly interesting example of stochastic integration with connections to local times, option p…
2
7
52
Using intuition from the discrete case, "Xᵤ downcrosses 0 when Wᵤ also downcrosses 0", and so u exists. However, I have no idea whether this holds in the continuous limit... Numerical simulations show that u exists, but I feel like this is due to numerical error?
0
0
0
Suppose now that Xₜ is started from ε: Xₜ ≔ ε + ∫₀ᵗ 1{Wₛ >= 0} dWₛ Since Xₜ = ε + max(W_t,0) - ½ L(t) and L(t) strictly increases only when Wₜ=0, does there exist a time u such that Xᵤ ≥ Wᵤ AND Xᵤ < 0? https://t.co/1aPExUdxuR
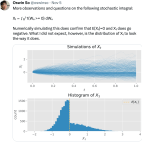
More observations and questions on the following stochastic integral: Xₜ ≔ ∫₀ᵗ 1{Wₛ >= 0} dWₛ Numerically simulating this does confirm that E[Xₜ]=0 and Xₜ does go negative. What I did not expect, however, is the distribution of Xₜ to look the way it does.
2
1
15
More observations and questions on the following stochastic integral: Xₜ ≔ ∫₀ᵗ 1{Wₛ >= 0} dWₛ Numerically simulating this does confirm that E[Xₜ]=0 and Xₜ does go negative. What I did not expect, however, is the distribution of Xₜ to look the way it does.
Small question about Ito integrals: Consider Xₜ ≔ ∫₀ᵗ 1{Wₛ >= 0} dWₛ where Wₜ is a Brownian Motion and 1 is the indicator. Xₜ is a martingale, so E[Xₜ] = 0. I would think that Xₜ is non-negative, but that doesn't seem to be true?
5
6
94
I realized theres a typo: I mean to put 1{X_s>=0} instead of 1{W_s>=0}. That changes the question significantly though.
1
1
6
Small question about Ito integrals: Consider Xₜ ≔ ∫₀ᵗ 1{Wₛ >= 0} dWₛ where Wₜ is a Brownian Motion and 1 is the indicator. Xₜ is a martingale, so E[Xₜ] = 0. I would think that Xₜ is non-negative, but that doesn't seem to be true?
4
3
32
Momentum Schrödinger Bridge is a nice framework for multi-marginal distribution matching (e.g. population modeling) that overcomes the stiff trajectories induced by most pair-wise distribution matching methods. Fun project with @iamct_r @MoleiTaoMath & Evangelos 🌉🌝
😀 #NeurIPS2023 Introducing our work #DMSB ( https://t.co/RO6UhEqALi)!
#DMSB is an extension of Schrödinger Bridge algorithm ( https://t.co/Lk5bHjqoOy and https://t.co/WiO8mXcHL1) in phase space to tackle trajectory inference task!
0
7
37
New blog post: Yet Another ICML Award Fiasco The story of the @icmlconf 2023 Outstanding Paper Award to the D-Adaptation paper with worse results that the ones from 9 years ago Please share it to start a needed conversation on mistakenly granted awards https://t.co/pIIl7BDBlX
parameterfree.com
Disclaimer: I deliberated extensively on whether writing this blog post was a good idea. Some kind of action was necessary because this award was just too unfair. I consulted with many senior peopl…
17
99
478
What is variational optimization? Why can continuous dynamics help? Optimization is already a profound field, what can it bring in? Check out blog https://t.co/RowKS3daUE Comment/Retweet/Like will be deeply appreciated! 1/6
itsdynamical.github.io
TL; DR Gradient Descent (GD) is one of the most popular optimization algorithms for machine learning, and momentum is often used to accelerate its convergence. In this blog, we will start with a...
1
42
159
We test EFPPO in simulation on challenging underactuated systems such as the "Top Gun: Maverick" inspired F16 fighter jet, and find up to ten-fold improvements in stability performance compared to baseline methods. (7/8)
1
0
0
However, the "cost structure" of the problem now changes. We prove a policy gradient theorem for this new cost structure, and combine this with the improvements from PPO to result in the *Epigraph Form PPO* (EFPPO) algorithm. (6/8)
1
0
0
Instead, we propose using the #epigraph_form, another technique of tackling constraints in constrained optimization. This introduces a scalar "cost budget" variable z. Importantly, the gradients of the policy do not scale linearly in this new variable, improving stability. (5/8)
1
0
0
While this works for "soft constraints", it leads to unstable optimization when we want safety constraints to always hold. In this setting, the Lagrange multipliers monotonically increase as long as safety constraints do not hold, destabilizing training. (4/8)
1
0
0
To solve constrained problems, we typically introduce a Lagrangian multiplier, then solve a minimax problem. In the constrained MDP literature, we can use reinforcement learning to solve this minimax problem. (3/8)
1
0
1
Many problems in robotics have a stability objective and a safety objective. To find a policy that satisfies both requirements, we can solve an infinite-horizon constrained optimal control problem, given some technical assumptions. (2/8)
1
0
0