However, we show that the *weight sharing* of a convolution kernel (or bias/nonlinearity) is only then coord. independent if this kernel is G-steerable (equivariant under gauge trafos). Coordinate independent convolutions are parameterized by such G-steerable kernels. [10/N]

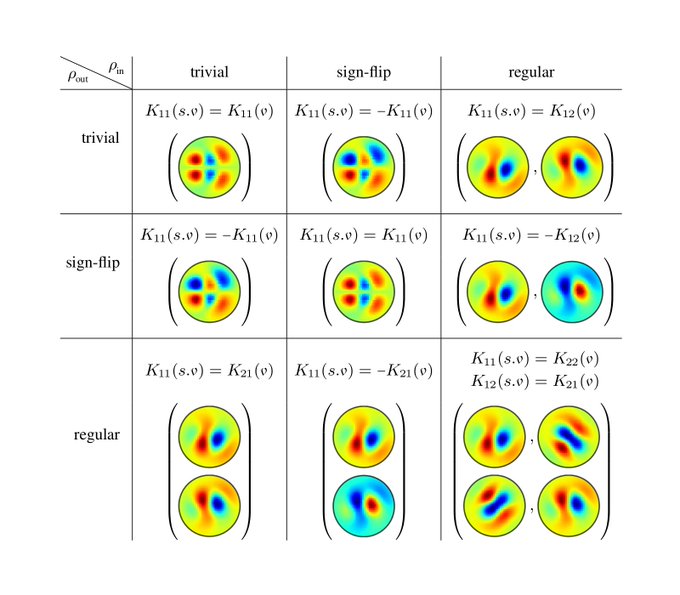
The fig. shows reflection-steerable kernels for different input/output field types of a convolution layer. Each combination results in some reflection symmetry of the kernels. [11/N]

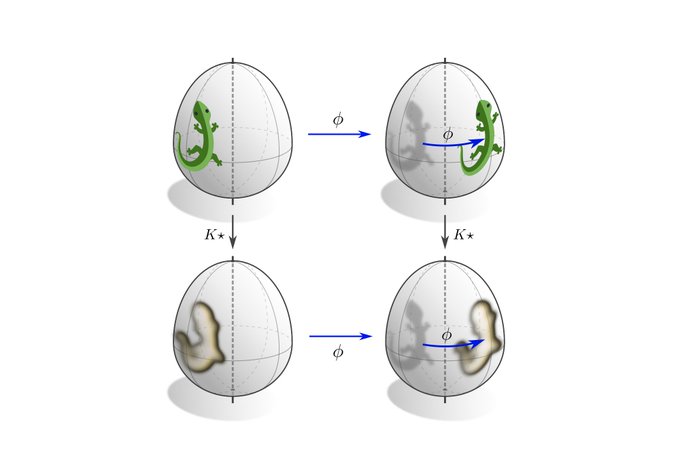
Besides being equivariant under local gauge transformations, coordinate independent CNNs are equivariant under the global action of isometries. This means that an isometry transformed input feature fields results in an accordingly transformed output feature field. [12/N]

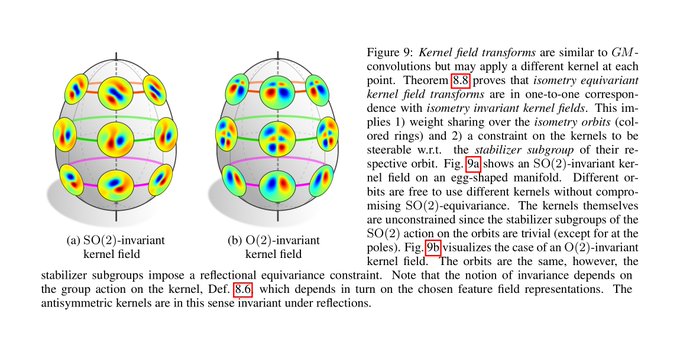
We find that isometry equivariance is in one-to-one correspondence with the invariance of the kernel field (neural connectivity) under the considered isometry (sub)group. Note that this only requires weight sharing over the isometry orbits, not over the whole manifold. [13/N]

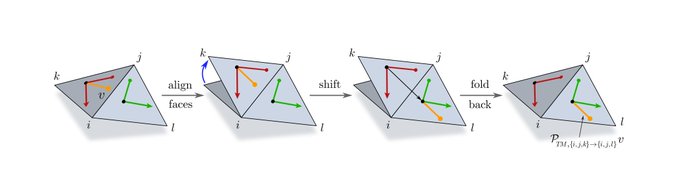
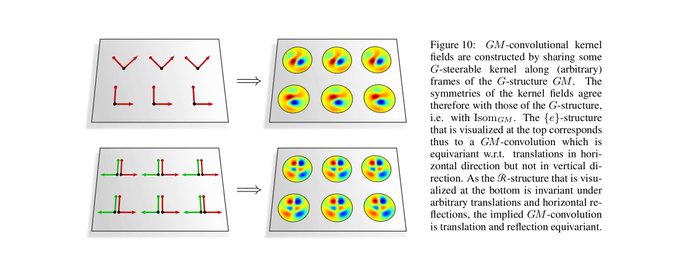
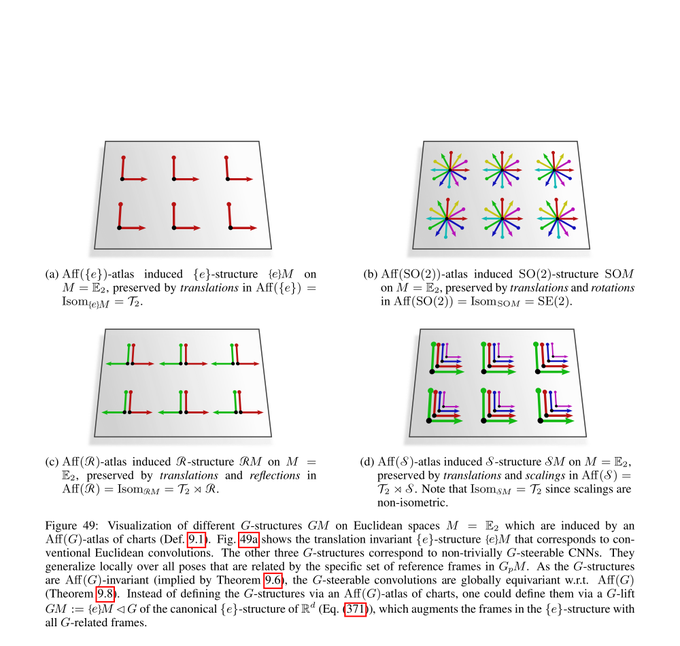
Coordinate independent CNNs apply G-steerable kernels relative to (arbitrary) frames of the G-structure, such that both have the same symmetries (invariances). It follows that our convolutions are equivariant w.r.t. the symmetries of the G-structure! (c.f. figs in [3/N]) [14/N]

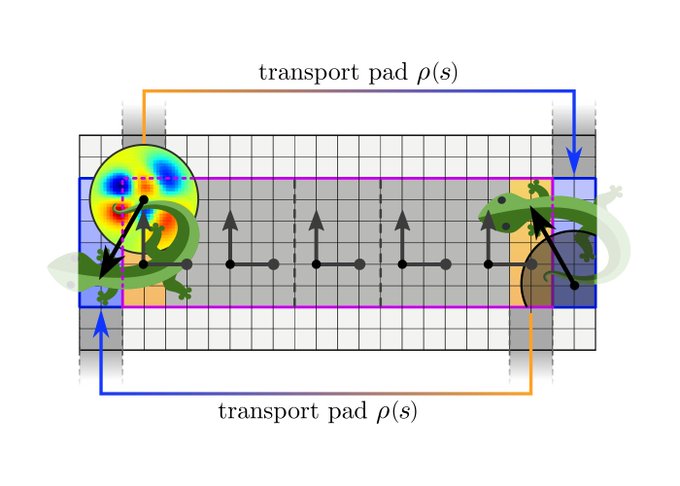
We implement and evaluate our theory with a toy model on the Möbius strip, which relies on reflection-steerable kernels. The code is publicly available at . [15/N]

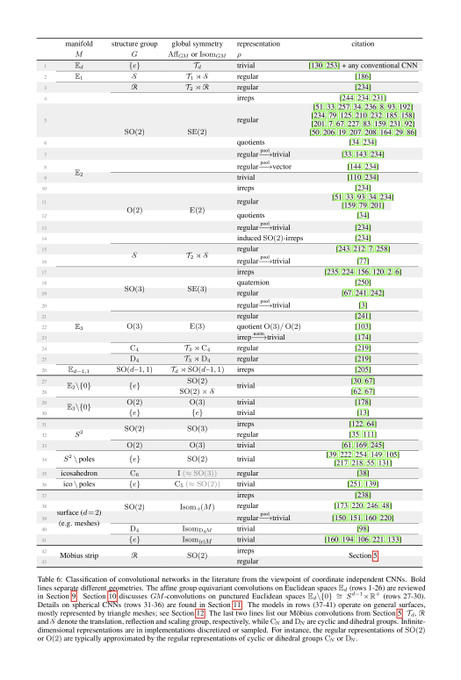
To demonstrate the generality of our differential geometric formulation of convolutional networks, we provide an extensive literature review of >70 pages. This review shows that existing models can be characterized in terms of manifolds, G-structures, group reprs. etc. [16/N]

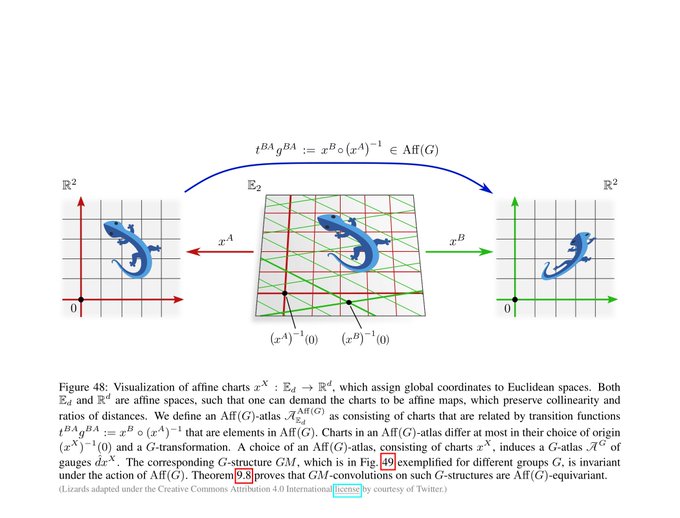
We first cover Euclidean coordinate independent CNNs. This is a special case where we can prove the models' equivariance under affine groups Aff(G) instead of mere isometry equivariance. [17/N]

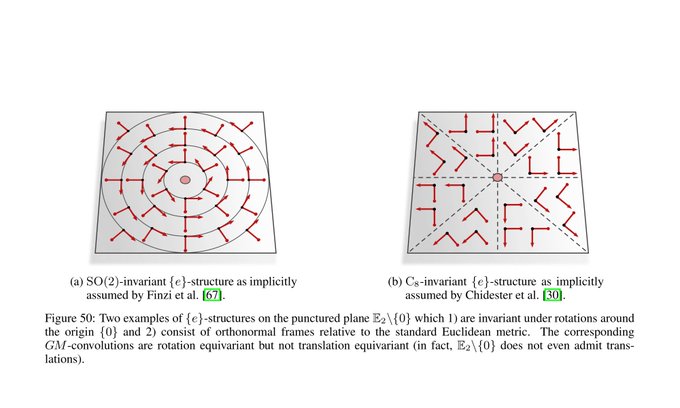
The more exotic convolutions which rely on the visualized hyperspherical G-structures are rotation equivariant around the origin but not translation equivariant. This covers e.g. the polar transformer networks of @_machc and @CSProfKGD . [18/N]

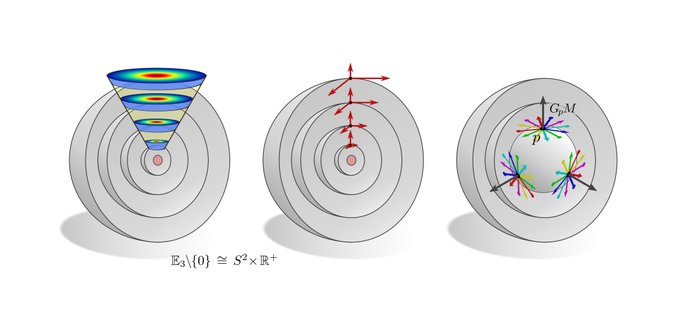
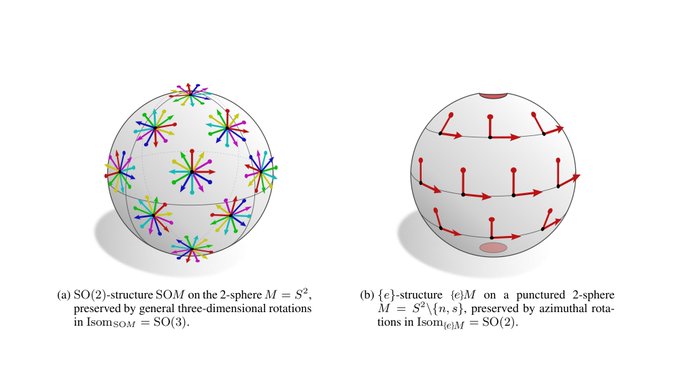
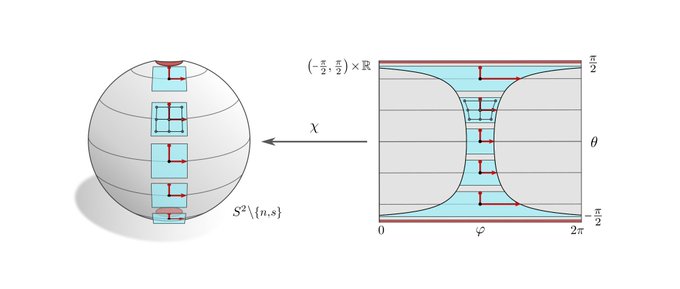
Spherical CNNs are usually either fully SO(3) equivariant or only equivariant w.r.t. SO(2) rotations around a fixed axis. They correspond in our theory to the visualized SO(2)-structure and {e}-structure, respectively. An alternative are icosahedral approximations. [19/N]

Note that our paper formalizes the "geodesics & gauges" part of the "Erlangen programme of ML" which was recently proposed by @mmbronstein , @joanbruna , @TacoCohen and @PetarV_93 : [21/N]

I am happy that this 2-year project is finally finished. Many thanks to my co-authors Patrick Forré, @erikverlinde and @wellingmax , without who these 271 pages of neural differential geometry madness would not exist! [22/N]