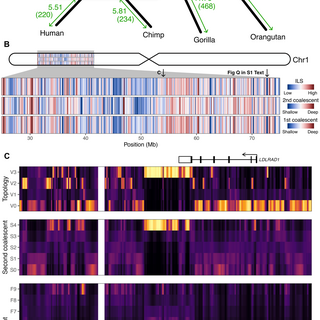
I am delighted to present TRAILS, a new hidden Markov model that.- reconstructs the speciation process (ancestral Ne and speciation times).- infers the multi-species ancestral recombination graph (ARG).Stay here for a brief summary of the paper! (1/17).

I cannot overstate how much of an incredible opportunity this is! The microbiome work of @DebrayReena and @jtung5 is cutting-edge and extraordinary. Come join our department here in beautiful Leipzig!.

RT @PLOSGenetics: Researchers from @AarhusUni_int & @Harvard introduce TRAILS — a hidden Markov model that accurately infers time-resolved….

This review is a collaborative effort between Asger Hobolth, Mogens Bladt, Andreas Futschik, and myself. I feel blessed to have teamed up with such amazing researchers! (18/18).

And if you are interested in using phase-type distributions, we have implemented a flexible and user-friendly R package called PhaseTypeR (17/18)

In this paper, we examine the advantages and limitations of PH distributions. We also discuss future directions, including statistical inference and maximum likelihood estimation, inhomogeneous PH distributions, and non-standard coalescent and mutational models (16/18).

Discrete PH distributions can be used for the mutational process—e.g., number of segregating sites or number of singletons (doubletons, etc.)—, or for the number of generations for a (potentially selected) variant to be fixed or lost in a Wright-Fisher population (15/18)

Moreover, PH theory is not restricted to the continuous case. By substituting exponentials by geometric distributions, we can build discrete PH distributions. These also have matrix-form formulas for the density function, cumulative distribution, mean and variance (14/18)

By using multivariate PH distributions, one can also calculate the covariance between different PH-distributed variables (13/18)

PH theory also provides a framework for obtaining PH distributions from another PH distribution using a vector of weights (or rewards), without the need to manually specify the new rate matrix (12/18).

This means that obtaining the distribution for the total branch length of the coalescent tree is straightforward by applying the same formulas to a new transition rate matrix (Q) that looks like this:

PH theory describes matrix-form formulas for the probability density function, cumulative distribution function, mean and variance of PH distributions. Regardless of what exponential rates are used in the rate matrix, the matrix-form formulas remain exactly the same (10/18)

For the case of the total tree height of 3 sequences, the transition rate matrix (Q) and initial probability vector (a) would look like this:

Luckily, we have phase-type (PH) distributions to save the day! PH distributions are defined as absorbing continuous-time Markov chains, represented with a transition matrix of exponential waiting times and a vector of initial probabilities (8/18).

However, for each specific case, the density and descriptive statistics (mean and variance) of such distributions need to be individually derived, which often involve complex mathematical calculations (7/18).

Many other quantities in population genomics are also sums of exponentials, such as the total branch length. In this case, each exponential will be weighted by the number of branches in each segment of the tree, i.e., a convolution of exponentials with rates 3/3=1 and 1/2=0.5.

Since the total tree height will then be the sum of two independent exponential random variables, it can be modeled as a convolution of two exponential distributions with rates 3 and 1. The mean and variance of this distribution can also be obtained with mathematical derivations.

But what if we are interested in obtaining a distribution of the total time until the most recent common ancestor of all three sequences? In this case, we will need to wait for the first two sequences to coalesce, and then the remaining two sequences can coalesce (4/18)

For three sequences, there are three different pairs of sequences that can find common ancestry. Thus, two of the three sequences will coalesce with an exponential rate of 3.

Following coalescent theory, two sequences find common ancestry, on average, Ne generations back in time, where Ne is the effective population size. Rescaling everything by Ne, the tree height of the coalescent between two sequences follows an exponential distribution of rate 1.

I’m thrilled to present our review paper about phase-type distributions in population genetics. Stay around for a quick explanation about how this family of distributions constitute an elegant alternative to classical coalescent derivations (1/18)