Do you use multilevel logistic regression? Do you use categorical and continuous predictors WITH interactions? Do you need to do a power calculation for your grant/article? Use my shiny app and get all the power you need! But first plz read my 1st twitter rant! 1/6

(1) The concept of statistical significance should be banned. (2) Bayesians should be forced to scientifically (not mathematically) justify their priors. (3) Causal inference is the scam of the century.

@rmarkdown @TDataScience p.s. our R package {InteractionPoweR} includes the ability to appropriately model covariate interactions in your interaction power analyses:

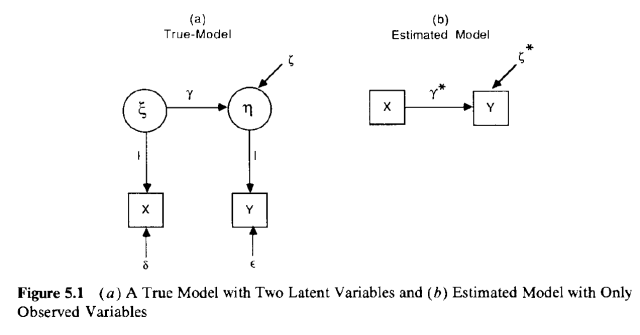
Days ago there was a most interesting discussion regarding the effects of measurement error on regression coefficients. Something that I think was missing was the *key* role that your measurement model has.

Here’s a fun blog post about the Fabius random variable. It’s kind of a random geometric sum and has some weird and wonderful properties. It’s CDF is infinitely differentiable but nowhere analytic (basically its Taylor series doesn’t “match” the CDF). 1/2 https://t.co/8i9WvRkqqx

Our new R package is mind-blowing! Are you interested in Large Language Models in R? Check out the example below. Task: automatic theme identification. Two synthetic stories generated via GPT-4: Story 1: "In the modern retelling of "Alice in the Wooderlands," Alice is a

'Graduate students need more quantitative methods support', a Comment by Andrea L. Howard (@DrAndreaHoward) Web: https://t.co/GviK7HnTQ1 PDF: https://t.co/Bbbx9WhuUD

I love seeing more simulation replications (our field needs this desperately) but evaluation of generalizability is so important! Simulators need to be aware that their one method of generating non-normal data (or some other factor) may not give the same results as other methods.

It's time for "Constraints on Generality" statements in simulations!

non-normalities do *we* find in our everyday research and which algo can better reproduce *those* types of non-normalities. I.e., I'm a psychometrician. 99.9% of my data are categorical. Care to guess which distributions I simulate the most from? 🫢 12/12

theory likelihood? I could be wrong, but I've never seen that done. Overall, Id say the idea that I keep on reminding people is: there is only *1* way to be normally distributed and an *infinite* number of ways to be non-normally distributed. The question is which kinds of 11/12

maximum likelihood approach retain its asymptotic properties (i.e., no inflation of Type I error among others). This opens up a whole area of research like "what happens when you use corrections in the presence of non-normality that doesn't actually influence the normal 10/12

robustness that can *only* be tested with the IG method ( https://t.co/TXR19zXbPa) The result is simple, elegant yet provocative: there are multivariate non-normal densities for which, EVEN in the presence of non-zero univariate AND multivariate kurtosis, the normal theory 9/12

ASYMPTOTE But what about when the results are not asymptotic? Well, we now know that different non-normalities can behave different Especially the Independent Generator (IG) method. This one taught me something that I had never encountered before: the concept of asymptotic 8/12

create problems, like inflated Type I error rates, not all "non-normalities" did so at the same level for finite sample sizes. The theory of SEM establishes the connection between excess kurtosis and the chi square test of exact fit. So we know we'd see an inflation IN THE 7/12

if you're used to working with multivariate, non-normal data: not all multivariate "non-normalitieS" (<--whatever that means, LoL) are created equal As you can see below (and much more in the paper) although the trend across *all* methods is common (i.e., non-normality can 6/12

99.999..% of soc scientists would use in any given scneario Although really, something like 99.999...888..% of soc scientists would just use the Fleishman method What did we find? Well, some really cool stuff. But really, the take-home message is probably somewhat expected 5/12

@mahnyunh @BD_Zumbo out what I wanted to know. And boy, was it interesting! We investigated 6 data-generating algorithms that can simulate some form of multivariate non-normality. From copula densities to power polynomial transformations, to the old NORTA approach... we tried what I'd argue 4/12

@mahnyunh about my research into the 5th order polynomial transform (for context. co-authored w/ @BD_Zumbo : https://t.co/2quLyY3NXD) I was quite surprised other ppl were interested in this area (there arent that many of us for... "reasons") so I jumped at the idea of finally finding 3/12

I couldn't help but wonder what would happen if we took the same idea, but brought it to the world of Monte Carlo simulations: One model, many data-generating algorithms. What would happen? Well, all of that was just an idea until @mahnyunh (co-author) emailed me asking 2/12

HA! @letsnotbehayest got the scoop today, but I would like to introduce all of you to this most interesting paper that had been in the back of my mind for a while. Context: Remember *that* "many analysts" paper (now a classic)? When I was reading it 1/12