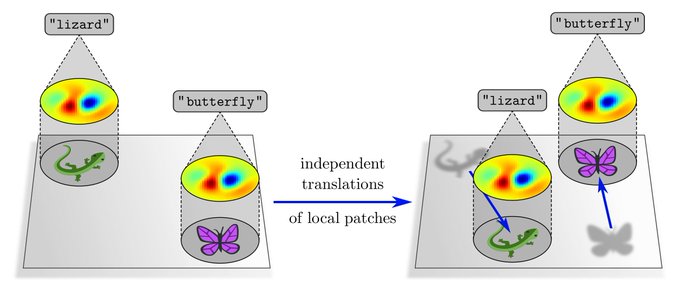
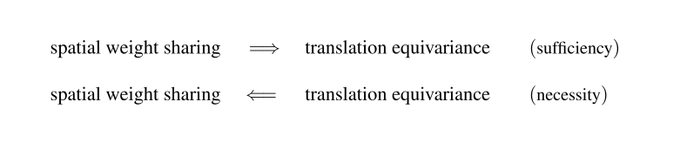A shortcoming of the representation theoretic approach is that it only explains global translations of whole feature maps, but not independent translations of local patches. This relates to local gauge symmetries, which will be covered in another post.
[11/N]
0
0
8
Replies
This is the 2nd post in our series on equivariant neural nets. It explains conventional CNNs from a representation theoretic viewpoint and clarifies the mutual relationship between equivariance and spatial weight sharing.
👇TL;DR🧵
1
64
309
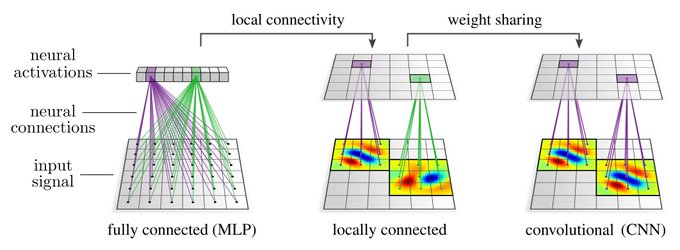
CNNs are often understood as neural nets which share weights (kernel/bias/...) between different spatial locations. Depending on the application, it may be sensible to enforce a local connectivity, however, this is not strictly necessary for the network to be convolutional.
[2/N]
1
0
11
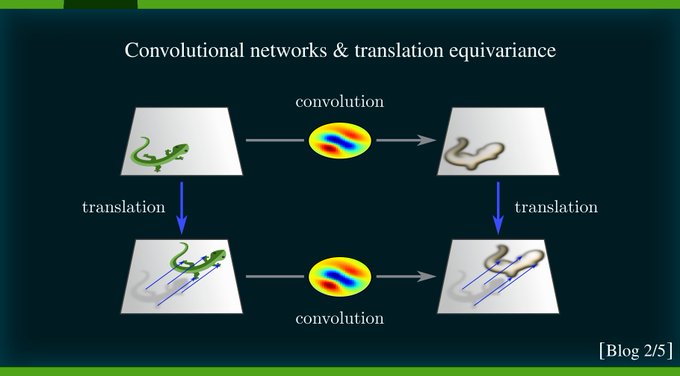
Imagine to shift the input of a CNN layer. As the neural connectivity is the same everywhere, shifted patterns will evoke exactly the same responses, however, at correspondingly shifted locations.
[3/N]
1
0
7
This "engineering viewpoint" establishes the implication
weight sharing -> equivariance
Our representation theoretic viewpoint turns this around:
weight sharing <- equivariance
It derives CNN layers purely from symmetry principles!
[4/N]
1
1
9
Feature maps with c channels on R^d are functions F: R^d -> R^c.
Translations t act on feature maps by shifting them: [t.F](x) = F(x-t)
The vector space (function space) of feature maps with this action forms a translation group representation (regular rep).
[5/N]
1
0
4
We define CNN layers simply as any translation equivariant maps between feature maps. Such layers are generally characterized by a translation-invariant neural connectivity, i.e. spatial weight sharing.
Some examples:
[6/N]
1
0
4
In general, linear layers may have different weight matrices at different locations. However, equivariance enforces these weights to be exactly the same, i.e. it implies convolutions.
[7/N]
1
0
3
In principle one could sum a "bias field" to feature maps, i.e. apply a different bias vector at each location. Equivariance forces this field to be translation-invariant, i.e. the same bias vector needs to be applied at each location.
[8/N]
1
0
4
Similarly, one could apply different nonlinearities at different locations, but equivariance requires them to be the same.
[9/N]
1
0
4
A benefit of the representation theoretic viewpoint is that it generalizes to other symmetry groups, e.g. the Euclidean group E(d). The next blog post will explain such generalized equivariant CNNs and their generalized weight sharing patterns.
[10/N]
1
0
5