The book brings together our findings on the representation theory and differential geometry of equivariant CNNs that we have obtained in recent years. It generalizes previous results, presents novel insights and adds background knowledge/intuition/visualizations/examples.
[2/N]
1
1
26
Replies
We proudly present our 524 page book on equivariant convolutional networks.
Coauthored by Patrick Forré,
@erikverlinde
and
@wellingmax
.
[1/N]
28
252
1K
The 1st part covers classical equivariant NNs.
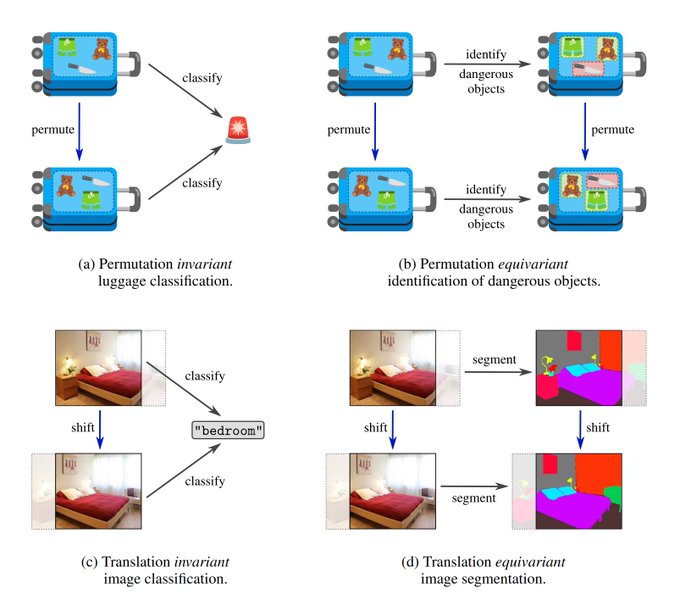
It starts with a general introduction to equivariant ML models, explaining what they are, why they enjoy an enhanced data-efficiency and how they can be constructed.
[3/N]
1
1
21
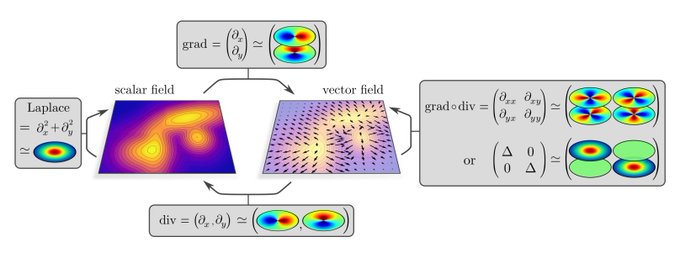
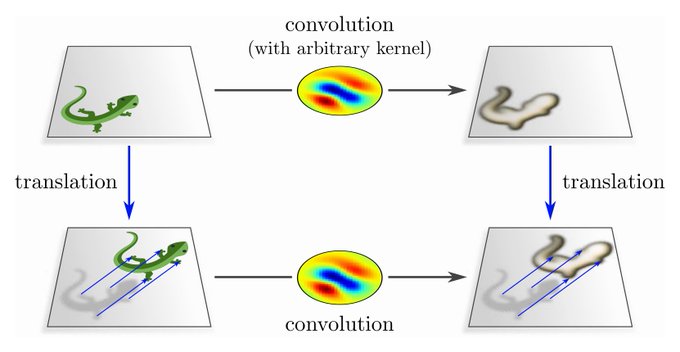
Next, we revisit conventional Euclidean CNNs, formalizing them in a representation theoretic language. We *derive* typical CNN layers (conv/bias/nonlin/pooling) by demanding their translation equivariance. Specifically: translation equivariance ⟺ spatial weight sharing.
[4/N]
1
1
17
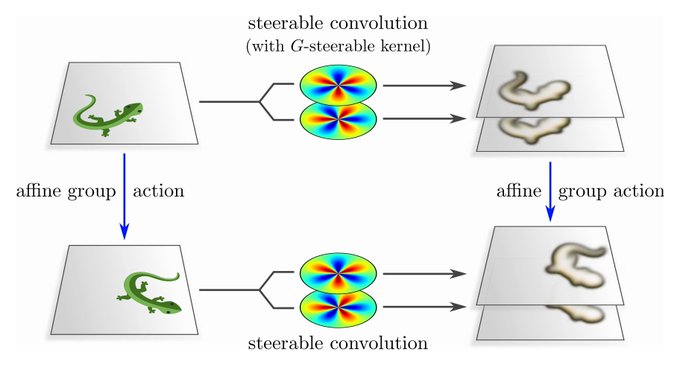
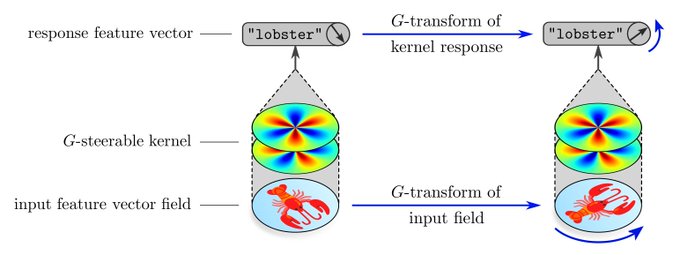
"Steerable CNNs" extend this approach to more general affine transformations (rotations/reflections/scaling/shearing/...). Besides spatial weight sharing, affine equivariance requires additional G-steerability constraints on kernels/biases/etc.
This chapter contains ...
[5/N]
2
1
17
... results that were known for years but have never been published: It covers transformations beyond isometries, adds derivations for various network operations, and proves that group convs are a special case of steerable convs. So far, all of these were unproven claims.
[6/N]
2
1
17
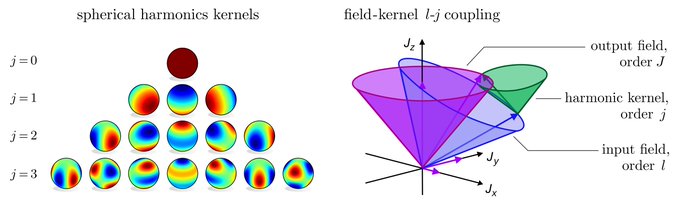
The following chapter is entirely devoted to G-steerable convolution kernels. It provides an intuition through simple examples, discusses their harmonic analysis, and addresses implementation questions.
[7/N]
1
2
14
The final chapter on Euclidean CNNs presents empirical results, demonstrating in particular their enhanced sample efficiency and convergence.
If you would like to use steerable CNNs, check out our PyTorch library escnn
(main dev:
@_gabrielecesa_
)
[8/N]
1
1
24
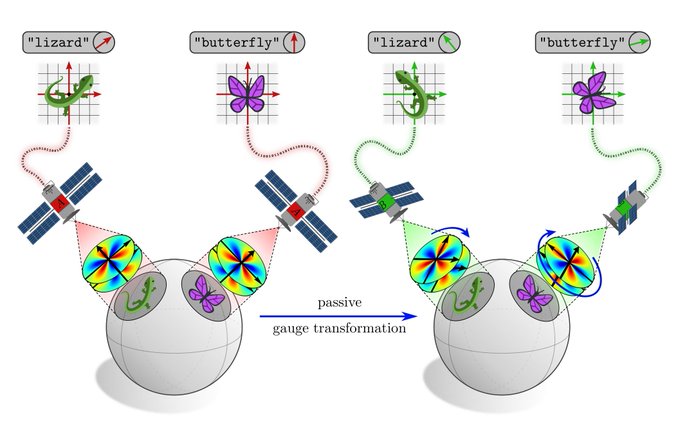
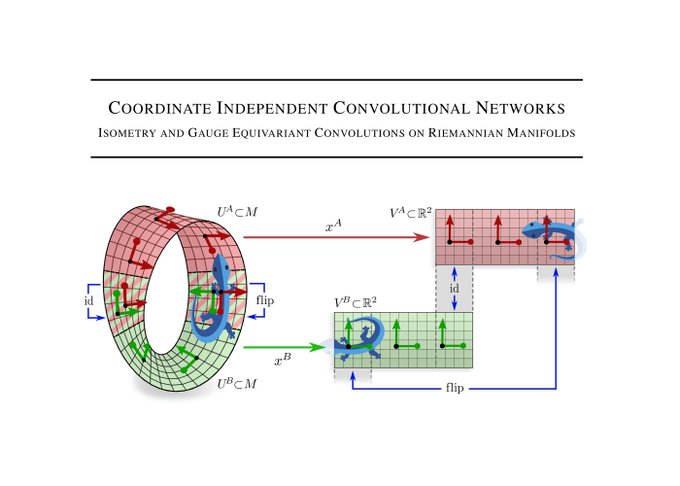
The following parts of the book generalize steerable CNNs
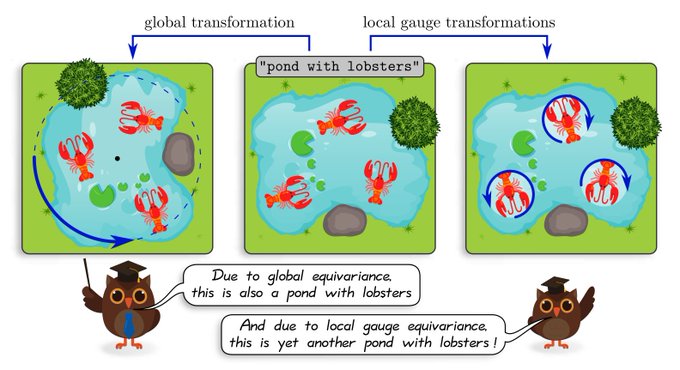
1) from Euclidean spaces to manifolds and
2) from global symmetries to local gauge transformations.
The gauge freedom lies thereby in the choice of local reference frames rel. to which features/layers are expressed.
[9/N]
1
1
16
These parts are based on our preprint on Coordinate Independent CNNs. Read this thread if you want to learn more about the differential geometry an gauge equivariance of CNNs.
[10/N]
Happy to announce our work on Coordinate Independent Convolutional Networks.
It develops a theory of CNNs on Riemannian manifolds and clarifies the interplay of the kernels' local gauge equivariance and the networks' global isometry equivariance.
[1/N]
24
324
1K
1
0
11
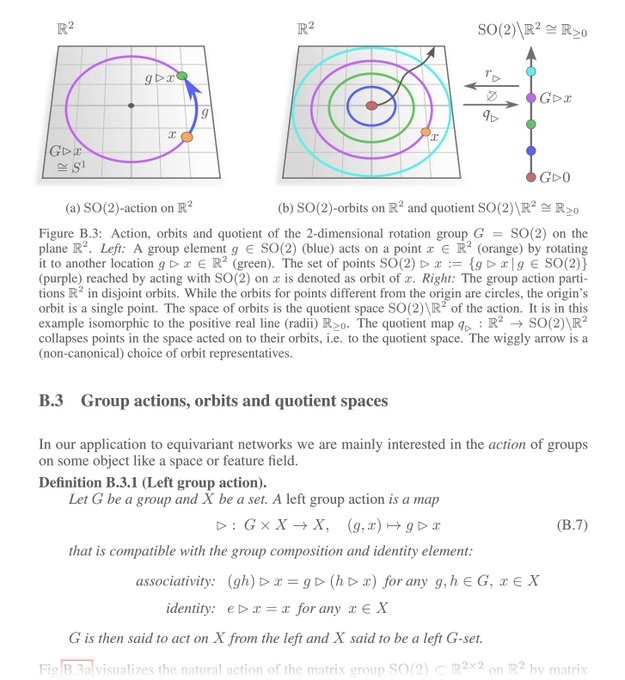
We also added an appendix on group and representation theory, intended to introduce the maths behind equivariant NNs to deep learning researchers. Defs. and results are made tangible via visualizations/examples and by discussing their implications for equivariant NNs.
[11/N]
1
1
15
If you would like to get an overview and simple introduction, check out the book's preface. It is written in blog-post style and aims to convey the basic ideas via visualizations.
[12/N]
>>> 209
1
1
20
In addition, I will soon release a series of blog posts that will cover the topics mentioned here in greater depth. Stay tuned!
[13/N]
0
1
23