A random memory: when I was an undergrad I went to an optics professor for advice; one question I asked was whether I could do research in theoretical optics. He looked at me with disgust and said, "there's nothing left to do in theoretical optics.".

The long-term goal is to build a bridge from introductory quantum optics to my current research, although the bridge is going nowhere and neither sturdy nor accessible at the moment.

Quantum Optics Lecture Notes v0.4:. A4 size: Letter size: Added some appendices on open quantum systems and classical statistics. Updated the appendix on probability.

Singapore is the hottest place to do physics now!.

It's useless because it assumes an estimator and you might as well compute the error directly. An inequality is useful only if the bound is easier to compute than the thing you are bounding, or the bound has some independent significance. (n/n).

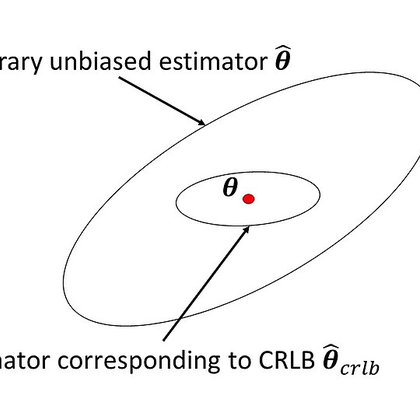
I heard many talks recently about bounds, and people would just write down inequalities and pretend that they are cool. One famous example is the Cramer-Rao bound for biased estimators (1/n).

Forgive me if I prefer quantum thermodynamics in the 70's [Lindblad (1975)]

Stop treating the academia like a game; it ends up embarrassing everyone at the institution and not just the offenders. Reputation is hard to build and easy to destroy.

(2/2).

I heard people are interested in quantum sensing of time-varying signals again, so it's time for yet another round of shameless self-promotion: (1/2).

Three recent experimental demonstrations of quantum-inspired superresolution spectroscopy:

Which typeface do you prefer for the text in a PDF?.

This will be handy for the new pope

research before tenure vs research after tenure.

Quantum Optics Lecture Notes v0.3.1. A4 size: Letter size: Updates after teaching PC4246 this semester. Clarifications of common issues, various improvements, and many bug fixes; see cover page for details.

Cool.

In the second part of the paper, I transform the Van Trees inequality into a time-independent Schrodinger equation so that an unfavorable prior can be solved and a bound on the worst-case convergence rate can be derived. (4/n).

I also found the best version among the Gill-Levit family of bounds (coinciding with Van Trees only in a Gaussian case). (3/n).

(2) Just as the Cramer-Rao bound can be written in the language of the Hilbert space, the Gill-Levit family of Bayesian Cramer-Rao bounds can be written in the language of differential geometry. (2/n).

Two pandemic-era papers I neglected to promote earlier: (1) For quantum objects that arrive randomly and rarely, the Poisson state is an approximation that leads to neat formulas for many information quantities. (1/n).