Today's Puzzle:

The @GlobalMathProj has teamed up with MLFTC of ASU presenting a course implementing GMP's core lesson design and teaching principles. We go through the principles in turn, in deep practical detail! e.g. **Principle 2: Tell a Story** A good story sparks curiosity, then builds

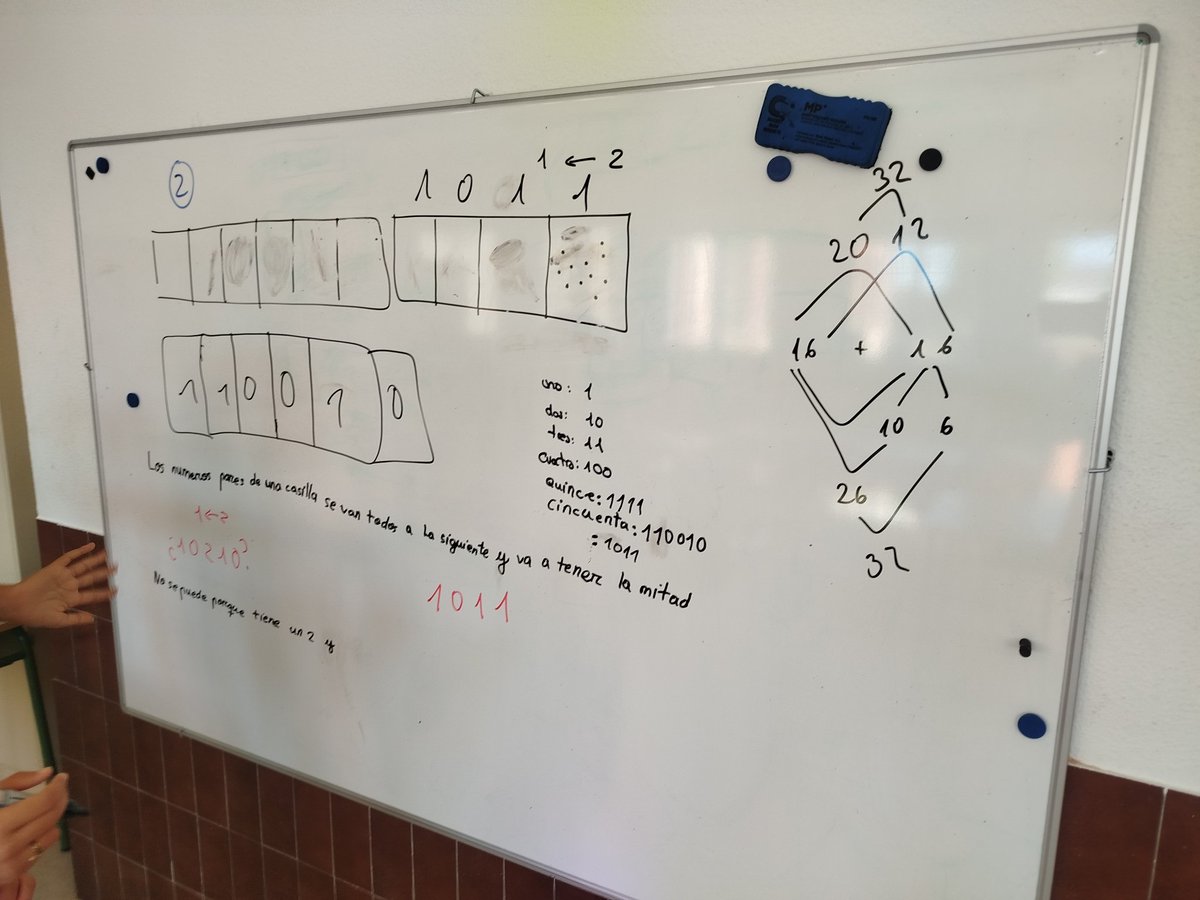
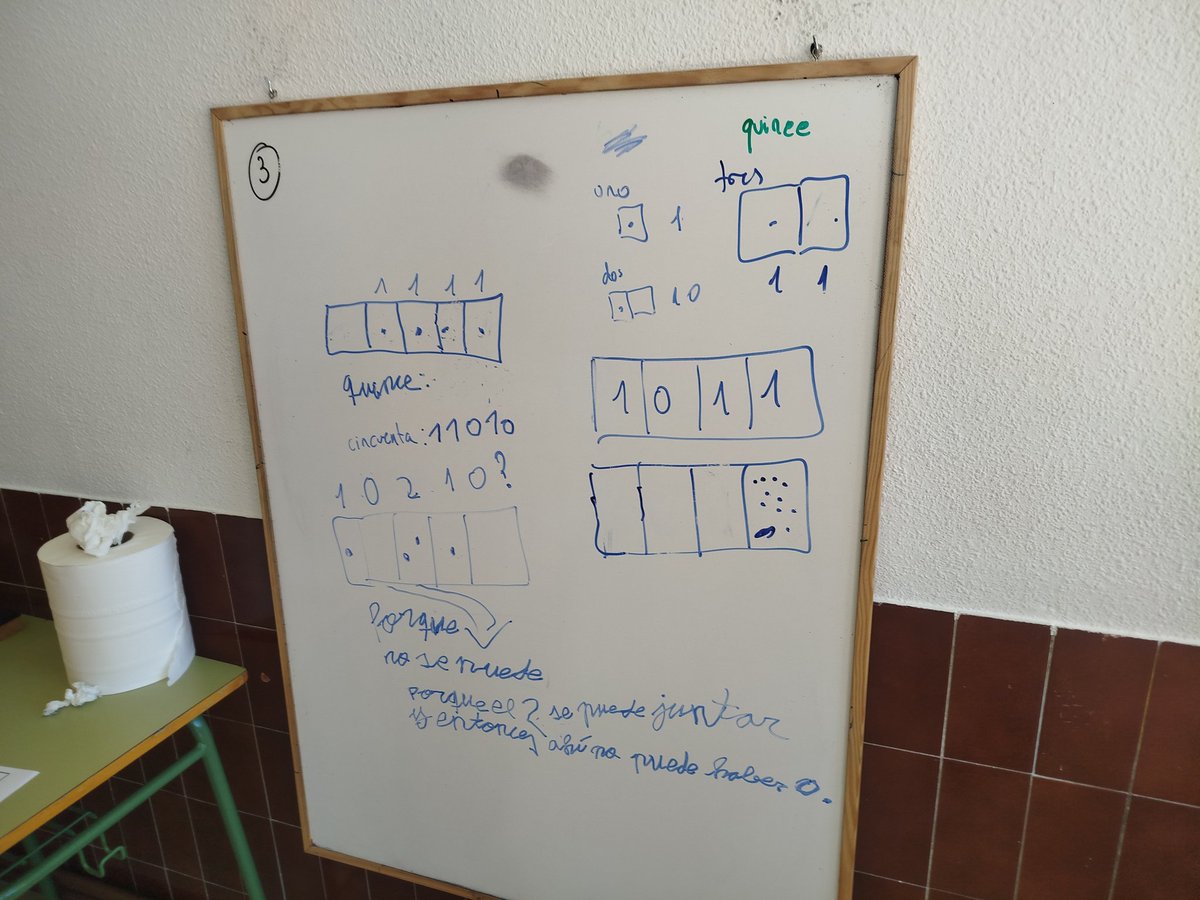
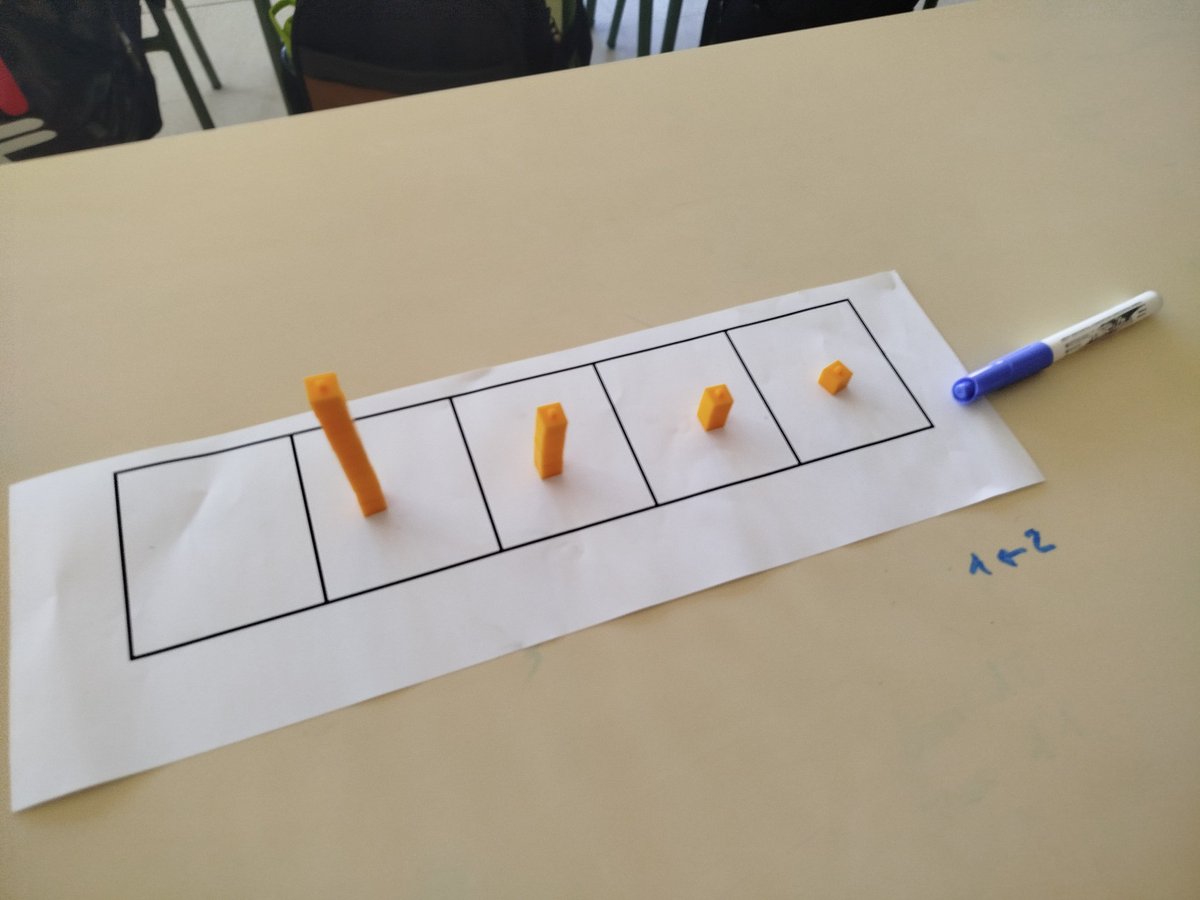
Comenzamos con los #ExplodingDots de @jamestanton. ¿Cómo se representan estos números en la "máquina 1<--2"? La secuencia completa (hasta operaciones con polinomios en Secundaria), aquí: https://t.co/zyisWBHyoB

Today's Puzzle:

Classic: Lines from corners to midpoints are drawn in a square. What is the area of the inner square formed?

Must every tiling of the plane with a given quadrilateral (edges meet along full edges) have 4 tiles surrounding each vertex? What if you tiled with two different quadrilateral tiles? Must it still be the case we have 4 tiles around each vertex?

One can tile the plane with a quadrilateral (tiles meet along full edges) so that each vertex is surrounded by 4 tiles. Is it possible to do the same with a triangle? With a pentagon?

Must every tiling of the plane with a right isosceles triangle (tiles meet along full edges) have each vertex surrounded by at least 4 triangles? Is there a tiling with a different triangle where some (all?) of the vertices are surrounded by just 3 triangles?

For any given tiling of the plane, is it possible to position the tiling on a coordinate system such that every point with integer coordinates lies strictly within the interior of a tile? (In other words, no tile boundary passes through any point with integer coordinates.)

From @BradBMath: There are N-gons that tile the plane with each tile surrounded by N distinct tiles (meeting edge-to-edge) for N = 3, 4, 5, 6. (And example for N=5 is shown.) Is there a 7-gon with this property?

Each triangle can tile the plane in a pattern that has two independent directions of translation symmetry. Possible to tile with only one direction of translation symmetry? No translation symmetry? With rotational symmetry but not translational symmetry?

There are convex triangles, quadrilaterals, pentagons, and hexagons that tesselate the plane. Prove no convex heptagon, however, can do the same.

Some tiling fun: There is a concave pentagon that tiles the plane. (Tiles meet along full edges.) Is there a concave quadrilateral that tiles? Concave hexagon? Concave N-gon for all N>6?

Some tiling fun: There is a 5-sided polygon that tessellates the plane. (Tiles need not align along full edges.) There are 5-gons that tile the plane. (Tiles always align along full edges.) Can you devise a concave pentagon that tiles?

Classic systems of eqns school algebra: I have a total of 787 dimes and quarters, adding to $123.70. How many quarters are there? a) How did someone get the total count of coins and total value of them without counting the quarters? b) A common sense way to solve the challenge?

A totally cool and clever virtual math escape room for students created by fellow Aussie, Peter Fox. Check it out and enjoy! https://t.co/AFegr4r0D1

Classic algebra textbook systems of eqns: I have a 20% saline and 35% saline solutions. I need an N% saline solution. What proportion of each should I mix to obtain this? Come up with two (three?) different ways to solve this without getting into a system of eqns!

Another approach to yesterday's puzzle: Why do the four regions above and below the blue line, left and right, have the same area?

Thinking through a classic for myself: The red and orange areas in each square have a combined area of 80 sq cm. The red area on left = red area on right. What is the red area?