Sosuke Ito (伊藤 創祐)
@ito_sosuke
Followers
3K
Following
139
Media
31
Statuses
922
東京大学理学系研究科附属生物普遍性研究機構(UBI)・准教授/物理学専攻A7(生物物理)/専門は非平衡統計力学、生物物理。 古典情報理論や情報の幾何学(情報幾何、最適輸送)と確率的or決定論的な非線形系における非平衡熱力学との関係を軸に理論物理の研究をしています。ありうる生物の情報処理の普遍法則を探究していきます。
東京大学 本郷キャンパス 理学部1号館
Joined August 2019
伊藤研では東京大学理学系研究科物理学専攻にて修士/博士課程学生を受け入れています。研究室に興味がある方はsosuke.ito@ubi.s.u-tokyo.ac.jpまでご連絡ください。 また予算の都合によりポスドクを募集している場合があります。ポスドクとしてくることに興味がある場合もお問合せください。
1
2
23
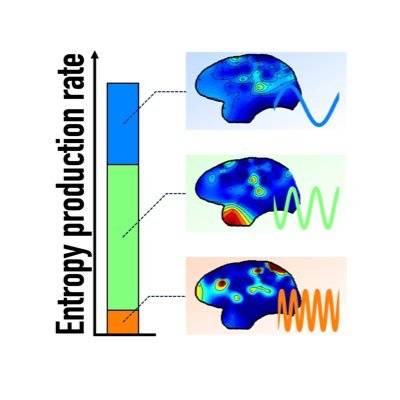
How do nonlinear oscillations generate thermodynamic dissipation? Our new arXiv preprint with @ito_sosuke and @oizumim introduces a Koopman-based framework that breaks down dissipation in nonlinear dynamics into contributions from oscillatory modes. https://t.co/XVBWFXMF6Z
5
51
323
Thrilled to share our latest preprint with @D_Sekizawa and @ito_sosuke! https://t.co/wHJGzVU52l We merge Koopman operator analysis with stochastic thermodynamics to uncover the oscillatory origins of thermodynamic dissipation in nonlinear systems. This framework pinpoints
arxiv.org
Nonlinear oscillations are commonly observed in complex systems far from equilibrium, such as living organisms. These oscillations are essential for sustaining vital processes, like neuronal...
How do nonlinear oscillations generate thermodynamic dissipation? Our new arXiv preprint with @ito_sosuke and @oizumim introduces a Koopman-based framework that breaks down dissipation in nonlinear dynamics into contributions from oscillatory modes. https://t.co/XVBWFXMF6Z
0
15
49
訂正: FitzHugh-Nagumoですね。Richard FitzHughなので。ハイフンの位置が変でした。 (なぜ人名の途中のHugh部分を大文字にするのか、理解していない)
1
0
5
個人的には、この新たな解析手法は近年発展してきた確率過程での熱力学の分野が、従来の非線形力学系の理解とうまく融合できる接点になればいいなあと思っています。
1
0
5
特に素朴な時間発展のPerron-Frobeniusに相当するKoopmanモードではなく、(時間発展寄与をexcessモードとして除いた上で)純粋な振動モードだけで構成されるHousekeepingの寄与に対する仮想的なダイナミクスでのKoopmanモードを見るというやり方は、Langevin方程式の解析手法としても新しいはずです。
1
0
5
前回の結果との大きな進展は、非線形系でもモード分解ができるというところにあります。前回の結果は線形で書けたので、線形代数から固有値モードで分解するということは(アイディアは別として)技術的な驚きは少なかったわけですが、今回の方法は非線形なLangevin系でできるところに価値があります。
1
0
5
解析は前のPRXの論文と同様に大泉研が素晴らしい解析をしていただきました。僕のほうではKoopman modeの話(dynamic mode decomposition)について色々と勉強しながら、熱力学として適切な取り扱い方やシンプルな理解の仕方を色々と考えることができました。
1
1
5
特に論文ではFitz-Hugh Nagumo方程式の非線形系にノイズを加えた状況で、Hopf分岐してリミットサイクルが現れるような状況や、確率共鳴が起こるような状況に適用しています。noise-inducedな分岐現象や非線形現象を熱力学の散逸の視点から捉えるための新たなツールになることを期待しています。
1
2
7
大泉研の関澤さんの結果がarXivに出ました。 https://t.co/FROQNr0iKP 維持エントロピー生成率を振動数ごとに(Koopman modeで)分解する話で、前回のPRXの結果の一般化になっています。特に非線形振動+ノイズのランジュバン系において、振動寄与がどう散逸に影響を与えるかを議論できます。
1
10
52
なので、本論文はNakazato-Itoで提案した情報熱力学を最適輸送で捉えようとする方向性に、さらに新たなアイディアが加わって精密した結果だと思うこともできます。色々とまだまだ展開できると思うので引き続き論文にしていければと思っています
0
0
7
この分解の順序の違いで結果は異なりえて、これがIto-Oizumi-Amariからずっと議論されてきた直交射影の順序問題ですが、実は今回の場合は、射影の仕方の性質から二つの方法間に良い不等式関係が成り立ちます。これが情報流の分解が2-Wasserstein距離による速度限界と関係してくる理由になってます
1
1
6
一方で別の方法もあり得て、まず全系のエントロピー生成率を情報熱力学的に部分に分解した後で、その部分エントロピー生成率の維持成分と過剰成分を探すやり方です。この方法だと過剰成分から2-Wasserstein距離と関係する概念が出てきて、これがいわばNakazato-Itoでやっていた方向性です
1
1
2
情報流の分解を生み出すには、まず全系のエントロピー生成率を過剰と維持部分に分解したのち、そこからさらに系を分割することによって情報流のうちの過剰成分と維持成分を取り出します。 この手法自体はNakazato-Itoではやっていない完全に新規なものです。
1
0
3
「Nakazato-Itoで議論した情報熱力学第二法則のタイトなバウンドとして議論した方向性をより深めたもの」 この表現も語弊を生みそうなのでもう少し説明をします。今全系のエントロピー生成率の分解を考えているわけですが、この分解の順序が実はとても重要です。
1
0
4
訂正 「情報流を時間変化を引き起こす過剰情報流と時間変化しない維持情報流」 は言葉足らずでした。 「相関の時間変化を引き起こす過剰情報流と、相関の時間変化を引き起こさない維持情報流」ですね。それぞれの量は、分布の変化に応じて時事刻々と変化します。
1
1
4
訂正 「情報流を時間変化を引き起こす過剰情報流と時間変化しない維持情報流」 は言葉足らずでした。 「相関の時間変化を引き起こす過剰情報流と、相関の時間変化を引き起こさない維持情報流」ですね。それぞれの量は、分布の変化に応じて時事刻々と変化します。
1
1
4
いわゆる分布が局在して緩和の過程でデーモンみたいな挙動をするのか、それとも二つの系の間で駆動されていることでデーモン的な挙動を部分系が担っているのかを、区別しながら議論できるようになります。これは情報熱力学の新たな理解につながるような重要なコンセプトになりうると思っています。
1
0
3
また物理的には、いわゆる「Maxwellデーモン」の描像を新しくしているのがポイントです。例えば今回情報熱力学第二法則を二つの形で一般化しているので、「excessの方では非デーモン」だけど「housekeepingの方ではデーモン」みたいな考え方をすることができます。いわゆるデーモン性の精密化です。
1
1
3
またこの論文は数理的にはテクニカルで面白く、情報熱力学の理論を線形代数の形で読み直せるようになっており、マルコフ過程における情報熱力学の現代的な理解を与えていると思います。以前山本くんとやったオンサーガ相反の理論で考えたグラフの縮約の話も線形代数の言葉で綺麗にまとまっています。
1
0
3