Mayank Chaturvedi
@imayank42
Followers
56
Following
98
Media
8
Statuses
32
ML engineer @GoogleDeepMind | Obsessed with math & AI. Exploring Gemma, on-device Gemini, and the power of compact LLMs.
Mountain View, California
Joined August 2024
I've discovered a powerful pattern in startup pitches. I was at a pitch event in San Francisco, and I noticed almost every single founder used the exact same psychological trick to open. They'd ask a simple question they knew 100% of the room would agree with. A couple of.
0
0
5
How many leaves does a random tree have? 🌳. I ran a simulation (using the Aldous-Broder algorithm) to find out, and the answer is beautifully simple. For a tree with N nodes, the expected number of leaves is ~N/e for large N. It's magical to see the simulation results perfectly
0
0
1
Amid all the noise these days, don't forget the og: The eigenvectors of the covariance matrix are the principal components.
1
0
6
RT @j_dekoninck: We just released the evaluation of LLMs on the 2025 IMO on MathArena! Gemini scores best, but is still unlikely to achieve….
0
40
0
RT @danielhanchen: Huge thanks to everyone who attended our @Google & @UnslothAI Gemma developer meetup yesterday! 🦥 Was amazing meeting yo….
0
6
0
RT @DynamicWebPaige: Next up: Mayank and the @ArtificialAnlys team sharing more about model customization, as well as Gemma 3 and 3n model….
0
1
0
RT @karpathy: The race for LLM "cognitive core" - a few billion param model that maximally sacrifices encyclopedic knowledge for capability….
0
1K
0
RT @osanseviero: I’m so excited to announce Gemma 3n is here! 🎉. 🔊Multimodal (text/audio/image/video) understanding.🤯Runs with as little as….
0
331
0
Super excited for the Gemma Developer Meetup in San Francisco this Thursday on 26th Jun! I'll be there, showcasing the power of Gemma models in my talk. Hope to see you there!.
0
1
5
RT @osanseviero: Gemma 3n is the first model with less than 10B parameters with a LMArena score above 1300 🔥. And yes, you can run it in yo….
0
95
0
The paper showed that, in contrast to conventional thinking about getting stuck in local optima, local critical points in high dimension are almost never valleys but are instead saddle points.
0
0
1
RT @penstrokes75: With the latest KerasHub release, you can now play around with Gemma3! Run it on JAX, TensorFlow, Torch. Whatever you wan….
0
6
0
Worked on the open source PyTorch implementation of Gemma 3. Try it out here:.!.
kaggle.com
Gemma is a family of lightweight, state-of-the-art open models from Google, built from the same research and technology used to create the Gemini models.
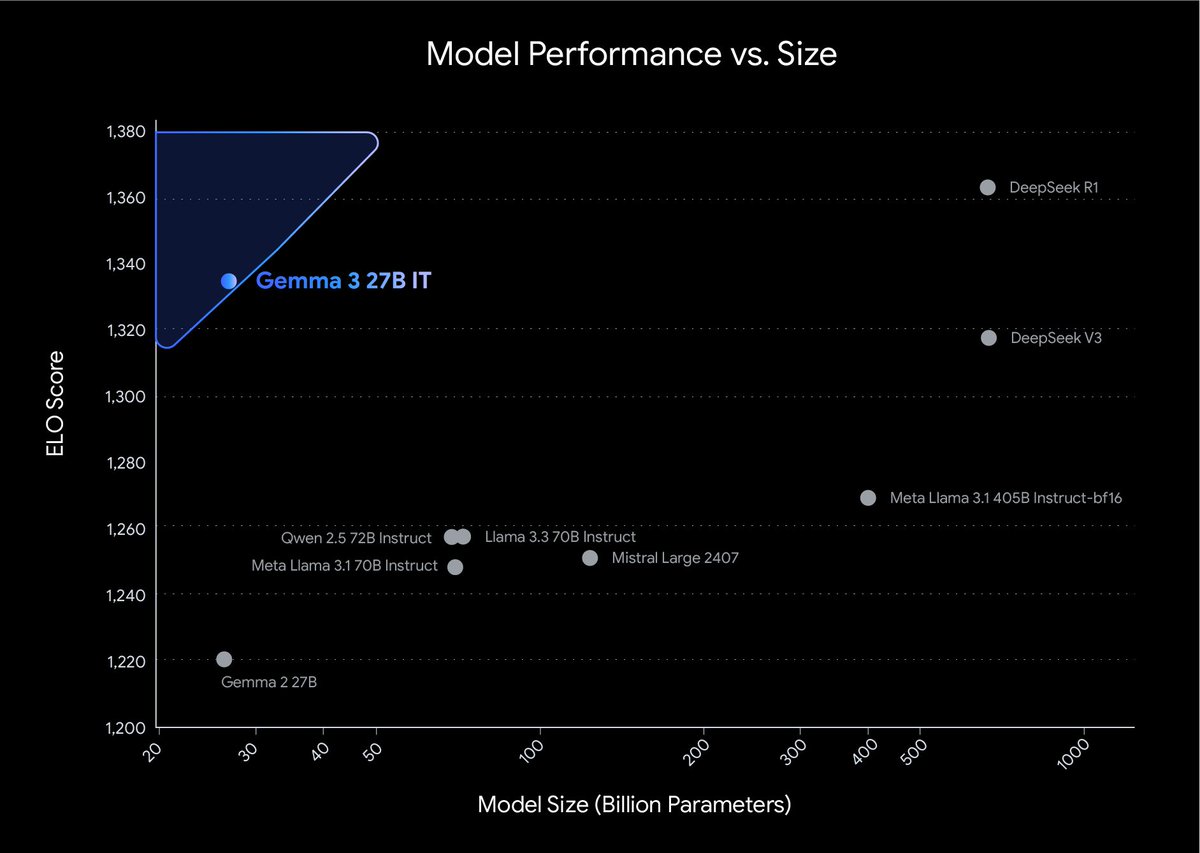
I’m so happy to announce Gemma 3 is out! 🚀. 🌏Understands over 140 languages.👀Multimodal with image and video input.🤯LMArena score of 1338!.📏Context window of 128k. Available in AI Studio, Hugging Face, Ollama, Vertex, and your favorite OS tools 🚀Download it today!
0
1
5
Secret santa derrangement is my fav christmastime puzzle.
0
0
0
Interdisciplinary at its best: This 2014 paper by @Yoshua_Bengio bridges Computational Geometry and Deep Learning, making a key theoretical step in explaining neural networks. Zaslavsky’s theorem helps bound their complexity.
0
0
0
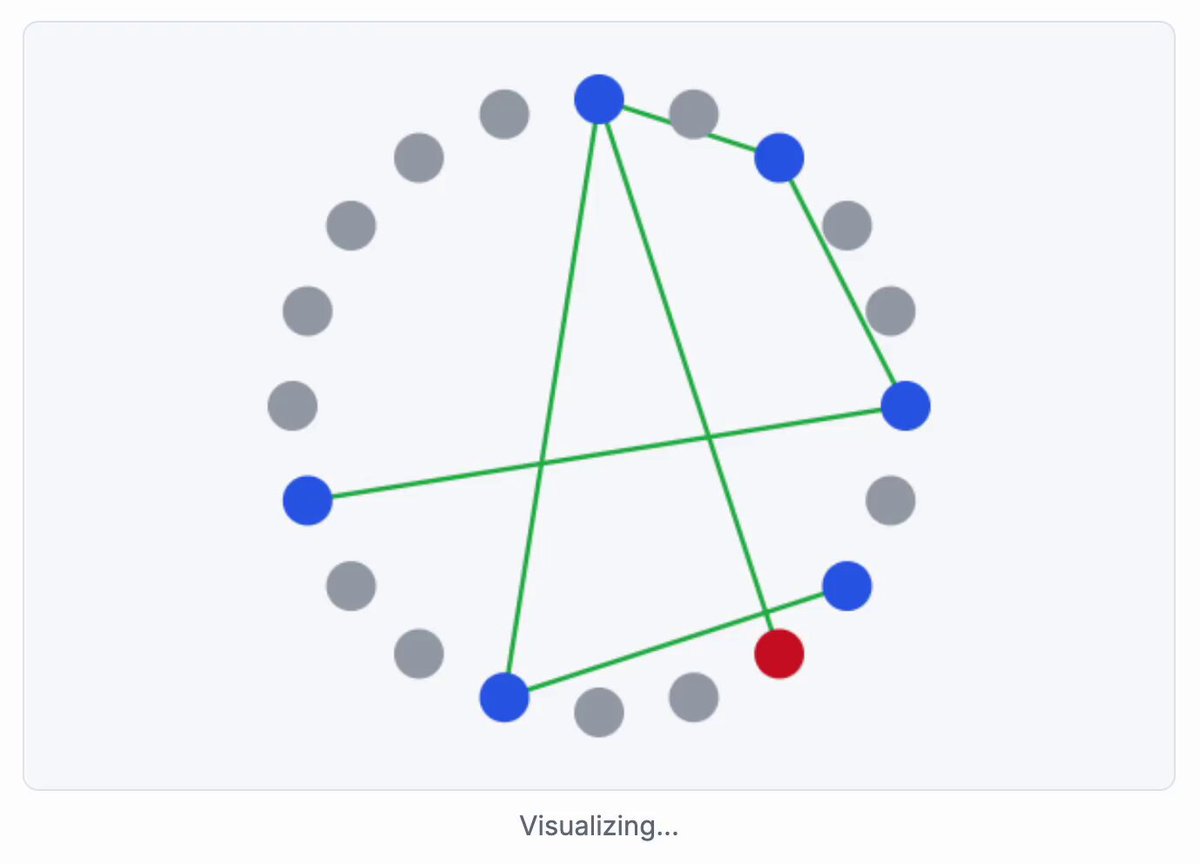
2024 has been an incredible year for combinatorics! Did you know in any group of 46 people, you’ll always find 5 mutual friends or 5 mutual strangers? . Read the groundbreaking paper: #Math #Combinatorics #RamseyTheory.
arxiv.org
We prove that the Ramsey number $R(5,5)$ is less than or equal to~$46$. The proof uses a combination of linear programming and checking a large number of cases by computer. All of the computations...
0
0
0
Among any 2n-1 integers, there is always a n sized subset that sums to a multiple of n.
0
0
0
Impressed by Raspberry Pi's new beta feature: Raspberry Pi Connect! Now you can access your Pi from anywhere in the world, out of the box. No screen or complex setup needed. Just remote control, simplified. Perfect for those who love Pi #raspberrypi.
0
0
1