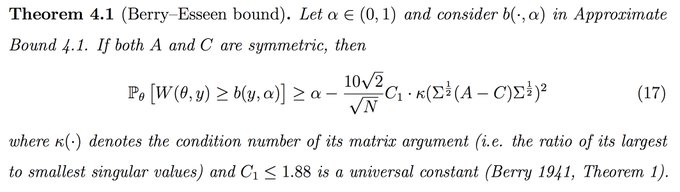One idea: Use a loss function L (e.g. squared error) and report the estimate with lower loss! I.e. use the more complicated T2 iff L(T*, T2(Y)) < L(T*, T1(Y)).
Problem: T* is unknown, so we can't operationalize this process.
1
0
1
Replies
We (
@skdeshpande91
,
@ta_broderick
and myself) have a new pre-print out now! It’s called “Confidently comparing estimators with the c-value”.
1
2
19
Ever used a hierarchical model to estimate a parameter and wondered if you’re actually doing better than a simpler baseline like maximum likelihood?
We present a method addressing this question!
1
1
1
Say you want to estimate an unknown parameter T* based on data Y. You have two potential estimates T1(Y) and T2(Y). T2 might be complicated (e.g. from a hierarchical model) and T1 is a more common baseline (e.g an MLE). When is it safe to abandon T1(Y) in favor of T2(Y)?
1
0
1
Enter the c-value! It quantifies how confident we are that T2(Y) achieves smaller loss than T1(Y). Informally, a high c-value reassures us that using the comparatively more complicated T2(Y) results in smaller loss than using T1(Y). (Thm 2.2).
1
0
1
We can even use the c-value to choose between T1 and T2: if the c-value exceeds a confidence level alpha, use T2. We show that we rarely incur higher loss as a result of the data-based selection than if we had just stuck with the default T1 (Thm 2.3).
1
0
1
To compute c-values, we construct lower bounds on the difference in loss L(T*, T1(Y)) - L(T*, T2(Y)) that hold uniformly w/ prob alpha. We demonstrate our construction w/ many examples including empirical Bayes shrinkage, Gaussian processes, & logistic regression.
1
0
1
We show c-values are useful for evaluating Bayesian estimates in a range of applications including hierarchical models of educational testing data at different schools, shrinkage estimates that utilize auxiliary datasets, and selecting between different GP kernels.
1
0
1
You might wonder: wait, what about RISK, i.e. the loss averaged over all possible realizable datasets? Well it turns out we can construct T1 and T2 where (A) T2 has smaller risk than T1 but (B) T2 incurs larger loss than T1 on *the majority of datasets*
1
0
4
Basically, loss averaged over all possible but unrealized datasets may not be close to loss incurred on the single observed dataset. c-values try to answer a different question: which estimator works better on *my observed dataset*.
1
0
2
Finally, constructing the uniform bounds on L(T*, T1(Y)) - L(T*, T2(Y)) is challenging & sometimes we need approximations. Fortunately,
@jhhhuggins
helped guide us towards some non-asymptotic bounds for Gaussian models (Thm 4.1), and an extension to logistic regression (Sec 5.2)!
1
0
1