New paper: Neural Rough Differential Equations !
Greatly increase performance on long time series, by using the mathematics of rough path theory.
Accepted at
#ICML2021
!
🧵: 1/n
(including a lot about what makes RNNs work)
3
90
495
Replies
(So first of all, yes, it's another Neural XYZ Differential Equations paper.
At some point we're going to run out of XYZ differential equations to put the word "neural" in front of.)
2/n
1
0
12
As for what's going on here!
We already know that RNNs are basically differential equations.
Neural CDEs are the example closest to my heart. These are the true continuous-time limit of generic RNNs:
3/n
1
0
7
But there's lots of other examples too, e.g. antisymmetric RNN, who use differential equations as inspiration for an RNN cell:
There's also been lots of other work on this going back to the 90s.
4/n
1
1
5
Best of all, if you look at the update mechanisms for a GRU or an LSTM -- but not simple "h_{n+1}=tanh(Wh_n + Wx_n + b)" Elman-like RNNs -- then they look suspiciously like discretised differential equations...
5/n
1
0
5
First moral of the story: you want to understand RNNs, or build better RNNs, then differential equations are the way to do it. <3
6/n
1
0
7
Alright, how do rough differential equations come into it?
These are differential equations, which (intuitively speaking...) have an input signal driving them -- but the input signal has wiggly fine-scale structure.
[Brownian motion, and SDEs, are a special case.]
7/n
1
1
6
Over in machine learning, what else has wiggly fine-scale structure?
Long time series!
Realistically, we probably don't care about _every_ data point in that long time series.
But each of those data points _is_ still giving us some small amount of information.
8/n
1
1
5
So, what to do? Throw away data? Selectively skip some data? Bin the data?
The answer (at least here) is that last one. Bin the data, very carefully, so that you get the most information out of the wiggles.
(...the least technical way possible of describing my PhD...)
9/n
1
0
7
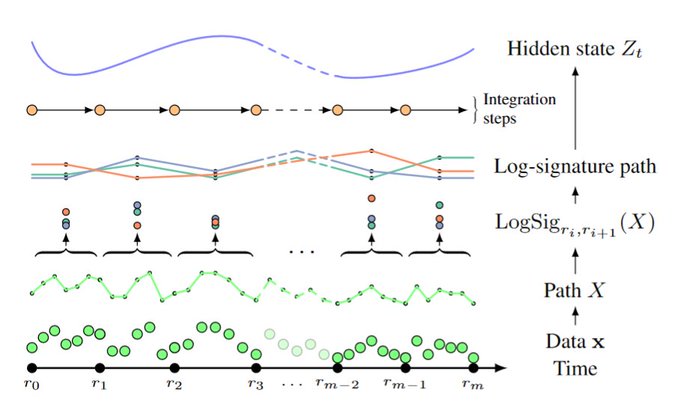
In particular, we use the "logsignature". This is a map that extracts the information that's most important for describing how an input path drives a differential equation.
...and as we've already discussed, RNNs are differential equations! <3
10/n
1
0
5
In fact, if you work through the mathematics...
(...see the appendix if you're really curious...)
...then doing all of the above corresponds to a particular numerical solver for differential equations, called the "log-ODE method".
11/n
1
0
8
Now remember, GRUs were just Euler-discretised differential equations. So were ResNets. So seeing another numerical solver shouldn't be too surprising!
12/n
1
0
7
In fact nearly anything worth using seems to look like a discretised differential equation...
A popular example from Twitter yesterday: MomentumNets. (
@PierreAblin
)
13/n
New paper out : Momentum Residual Neural Networks !
Introducing a new drop-in replacement for any ResNet that makes it invertible, thus saving loads of memory !
With
@m_e_sander
@mblondel_ml
&
@gabrielpeyre
Preprint :
Accepted at ICML 🍾🍾🍾
1/6
12
118
578
2
0
10
Returning to logsignatures: we get a way to feed really long data into anything RNN-like.
In this case we go full-continuous and use a Neural CDE, but any old RNN would work as well.
And because we've made things much shorter -- "extracted information from the wiggles" --
14/n
1
0
4
-- then all the standard problems with learning on long time series are alleviated.
No vanishing gradients.
No exploding gradients.
No taking a really really long time just to run the model...
(...looking at you, everyone I have to share GPU resources with...)
15/n
1
0
8
In our experiments we successfully handle datasets up to 17k samples in length.
(We could probably go longer too, but that was just what we had lying around...)
16/n
1
0
3
Anyway, let's wrap this up.
If you're interested in RNNs / time series...
If you're interested in long time series...
If you're interested in (neural) differential equations...
...then this might be interesting for you.
17/n
1
1
8
The paper is here:
The code is here:
If you want to use this yourself then the necessary tools have been implemented for you in torchcde:
18/n
1
1
14
Thank you for coming to my TED talk about RNNs and differential equations. :)
19/20
1
0
5
A huge thanks to James Morrill for taking the lead on this paper.
(Who unfortunately doesn't have a Twitter account I can link, so he's asked me to do this instead :) .)
20/20
1
0
3
Appendix for the physicist:
If you have a physics background, then you may know of "Magnus expansions". These are actually a special case of the log-ODE method.
21/20
1
1
6
Appendix for the stochastic analyst:
The rough path theory used here is super cool.
It gives you a pathwise notion of solution to SDEs:
And gives an easy universal approximation theorem for RNNs/CDEs!
(Appendix B)
22/20
2
1
9