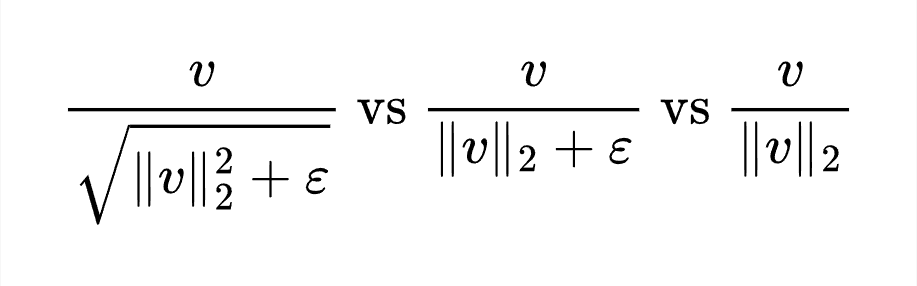I thought Procrustes referred to a mathematician

@stupdi_didot I forgot to add that r+eps, sqrt(r^2+eps^2) and max(r,eps) correspond to the ell1, ell2 and ell-infinity norm of the 2D vector (r,eps) respectively. Perhaps this could help with analysis or creating new ideas.

@stupdi_didot This is a very interesting alternative, v/max(r,eps). The Jacobian is still bounded, scale-free is preserved for eps>r, the only concern is that it is non-differentiable at r=eps, but you can use subgradients.

@stupdi_didot In short:.Use unbiased normalization if no backprop (e.g. optimizers) to preserve scale-free property.Use biased normalization with epsilon inside sqrt if differentiating (e.g. layer/batch-normalization) for numerical stability+simple implementation.Avoid epsilon outside sqrt.

@stupdi_didot Therefore, with the common ε_in^2=ε_out parameterization, the in(v|ε^2) normalization will be more numerically stable than out(v|ε) in the gradient

I'll clarify a point on in vs out.As noted by @stupdi_didot:. ||in(v|ε^2)||_2/√2 <= ||out(v|ε)||_2 <= ||in(v|ε^2)||_2. So with typical ε_in^2=ε_out.We see out(v|ε) shrinks more aggressively close to 0 than in(v|ε^2) (as seen in the vector field).

My personal conclusion is the following: No differentiation (e.g. optimizers), use dir for scale-free property In layer/batch normalization, as you need to backpropagate + numerical stability, use in (+ simpler implementation).

(To implement on GPU, in is well-behaved with no branching even for its derivative, while dir and derivative of out will need a mask.).

As you can see, the Jacobian of dir(v) has unbounded operator norm as ||v||_2 goes to 0, so you shouldn't be using it if you need to take derivatives

For v≈0 much smaller than epsilon (v<<ε), in(v) behaves approximately like r/sqrt(ε), while out(v) behaves approximately like r/ε. So here is a "fair comparison" of vector fields out(v|0.2) vs in(v|0.4)

Here is a summary table of in(v) vs out(v). Note that out grows faster for r near 0.

However, all norms proportional to the L2 norm on R^n are rotationally invariant. In fact, these are the only norms that satisfy this property. So this includes the RMS norm ||v||_2/sqrt(dim v). (see bonus at the end).

Notice that dir(v) is scale-free (positively homogeneous of degree 0), i.e. dir(cv)=dir(v) for any c>0 since a norm is positively homogeneous. This no longer holds for in(v|ε) or out(v|ε) for non-zero ε.

Let's define the following for convenience. dir(v)=0 at v=0 else v/||v||_2. Position of epsilon: inside square root for in(v), outside for out(v).

Note that the subdifferential (subgradient) of the Euclidean norm is set-valued at the origin. However, if we pick the zero vector at the origin, then we recover a generalization of the sign function, a direction function "dir(v)".

What are the effects of adding epsilon in the denominator in L2 normalization?.Typically, we say it's for numerical stability. But which choice to make and when?

In Muon, during dualization, we normalize the gradient matrix entrywise by the Frobenius norm to bound the spectral norm and ensure convergence. Have we compared the performance versus the geometric mean of the matrix norms induced by 1 and infinity vector norms (or the minimum)?

For anyone accessing this now, I have split the post into two parts as it was quite lengthy, so there is a new URL:.

Google is hiding the reasoning trace like OpenAI now??

Linear Algebra - A Geometric Crash Course. I am writing this crash course in my blog site in preparation for a blog series. I would appreciate your feedback on the format, e.g. the use of colored boxes, if you like it or prefer to use it more sparsely.